Hello friends of steemit continuing with my explanations on the science of mathematics today I want to refer to the limit of a function, all its main mathematical properties, and variables that are presented in this mathematical procedure, I invite all to observe this interesting educational post about the mathematical explanation - limit of a function

Limit of a function

The limit of a function is a fundamental concept of mathematical analysis applied to the functions. In particular, the concept applies in real analysis to the study of limits, continuity and derivability of real functions.

Intuitively, the fact that a function f reaches a limit L at a point c means that, taking points sufficiently close to c, the value of f can be as close to L as desired. The closeness of the values of f and L does not depend on the value acquired by f at said point c.

History

Although implicit in the development of the Calculus of the seventeenth and eighteenth centuries, the modern notation of the limit of a function goes back to Bolzano who, in 1817, introduced the bases of the epsilon-delta technique. However, his work was not known while he was alive. Cauchy expounded limits in his Cours d'analyze (1821) and seems to have expressed the essence of the idea, but not in a systematic way. The first rigorous presentation of the technique made public was given by Weierstrass in the 1850s and 18604 and has since become the standard method for working with limits.

Formal definition

Real variable functions

If the function f has a limit L on e we can informally say that the function f tends towards the limit L near if c it can be made as close as we want to by making it close enough to being distinct from.
The concepts close and sufficiently close are mathematically inaccurate. For this reason, there is a formal definition of limit that requires these concepts. Then it is said:

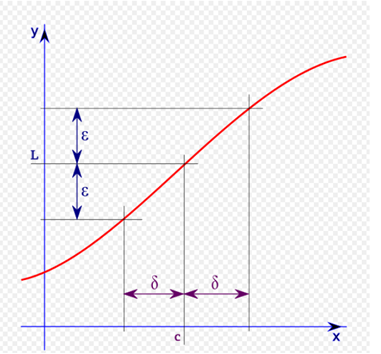
Display of the parameters used in the definition of limit.

The limit of a function f (x), when x tends to c is L if and only if for all e > 0 there is 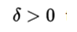such that for every real number x in the domain of the function, if 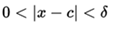so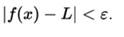

This, written in formal notation:

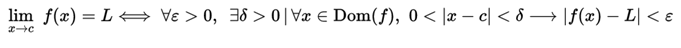
This is a strict formulation of the concept of the limit of a real function in a point of accumulation (or limit point) of the domain of the function and is due to the French mathematician Luis Cauchy.

The important thing is to understand that formalism does not do mathematical symbols, but the precision with which the concept of limit is defined. This notation is tremendously powerful, because it tells us that if the limit exists, then you can be as close to it as you want. If you can not get close enough, then the choice of & was not adequate

Let's see an example. Suppose you want to show that 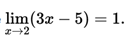The calculation of this limit arises by simple substitution, this is because the related function is continuous.

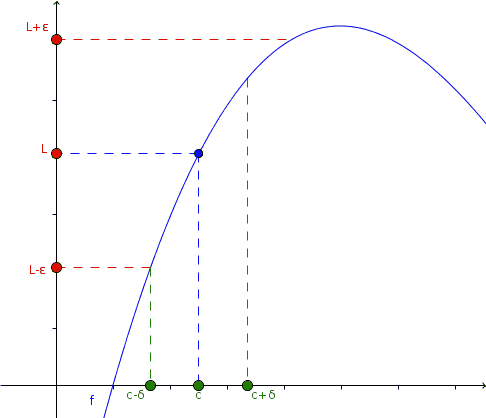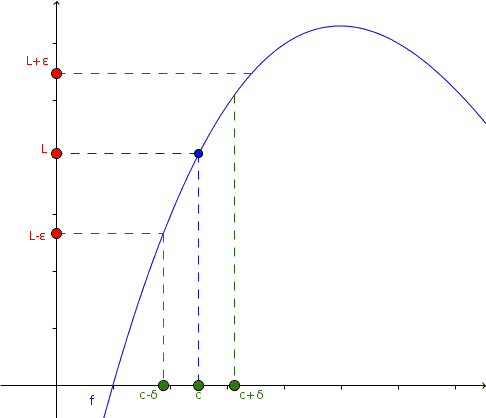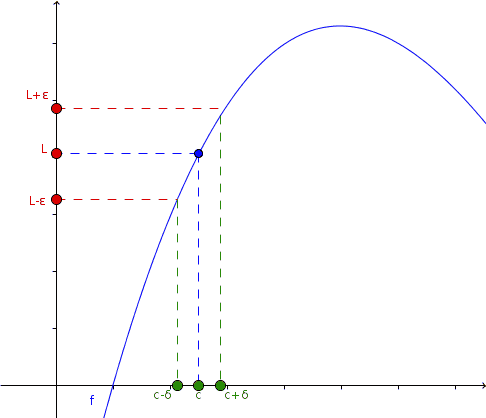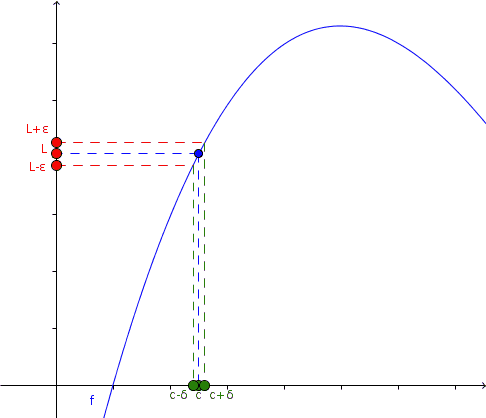
Taking arbitrary values of ε, we can choose a δ for each of these, so that f (x) and L come closer as x approaches c.

Demonstration

There are cases such as the Dirichlet function 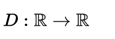Defined as:

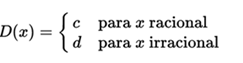
where there is no a number in the domain for which the 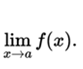To demonstrate the above statement, it is necessary to make use of the fact that each interval contains both rational and irrational numbers.

Sequential limit

It consists in defining the limit of a function in terms of the values it takes for successions contained in its domain.

A real function f has a limit L at a point x = c of its domain if for every sequence Xn that converges at this point c, the sequence f (Xn) converge to L.

In formal terms, if Xn is a sequence such that

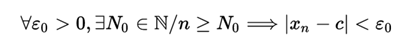
then f has limit L at x = c if and only if

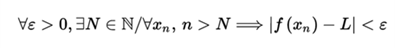
which is symbolized like this:

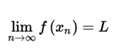
This definition in terms of successions is equivalent to the definition epsilon-delta of Cauchy.

Demonstration

The sequential limit provides a simple way to prove the non-existence of certain limits, such as the aforementioned one

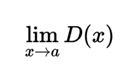
for them it is enough to take two different sequences that converge to point a:

1 . one that contains only rational numbers and
2 . another that only contains irrational
in this way, the function is forced to take two different values on successions that tend to the same point in the domain. Then, the limit does not exist.

Functions of two real variables

Given a function

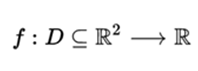
that each pair (x, y) of real numbers contained in set D assigns a real number z, it is possible to extend the definition of limit to this type of functions. Let (a, b) be an accumulation point of set D, it can be defined at the limit L of f at this point as follows.

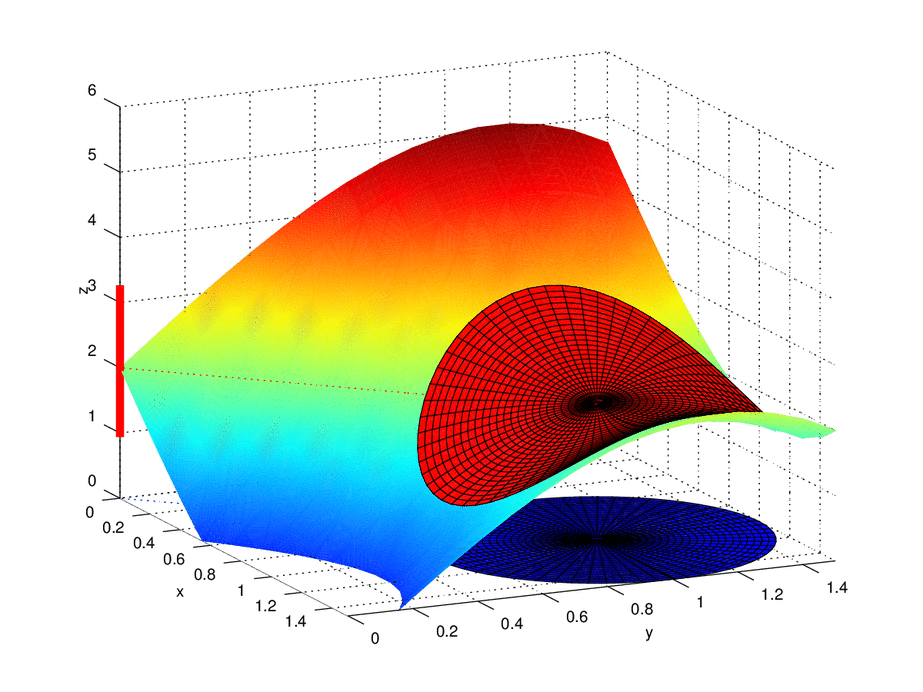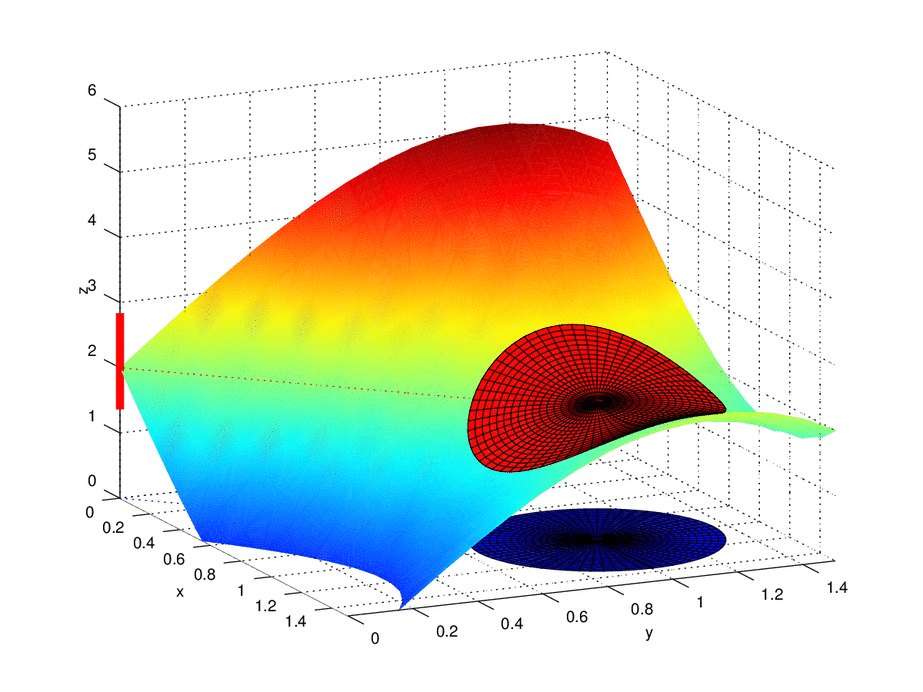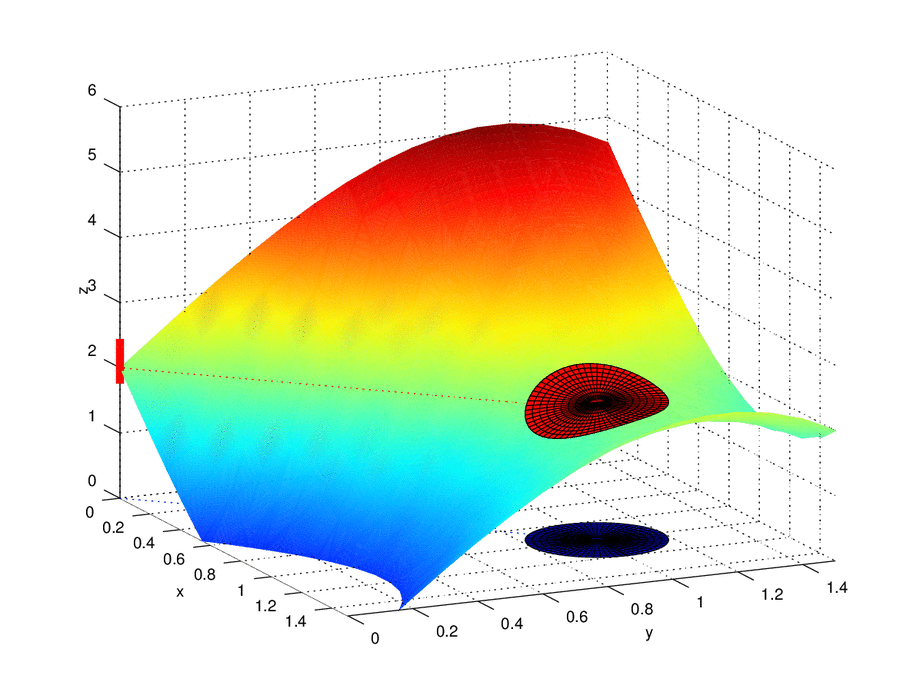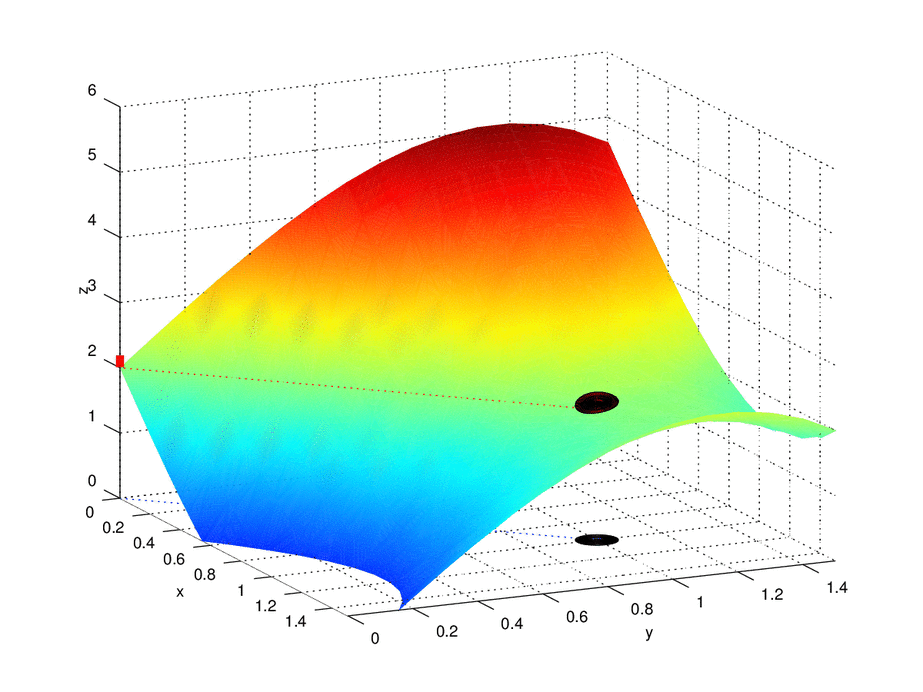
As the interval that surrounds L is refined, a smaller disk of radius δ can be taken, within which it is possible to approach point (a, b), without necessarily going through it.

The limit of a function f (x, y) when x tends to a and e tends ab is L if and only if for all ε> 0 there exists a δ> 0 such that for all pair of real numbers (x, y) in D it is fulfilled the implication

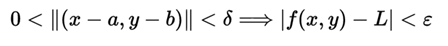
with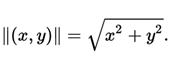

We will take as an example the following function

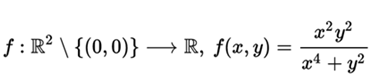
The point (0,0) is a point of accumulation of the domain of f, since any environment with center at this point contains others, different from the first, also belonging to the domain of the function.

For this function is fulfilled

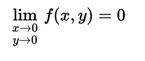
which can be demonstrated by definition.

Demonstration

If instead of a scalar function the vector field is taken

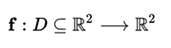
The definition of limit is analogous.

The limit of the vector field f (x, y) when x tends to a and e tends to ab is the vector L if and only if for all ε> 0 there exists a δ> 0 such that for all pair of real numbers (x, y) in D the following implication is fulfilled

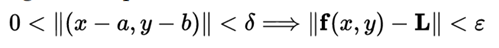
Infinite limits

There are several cases of limits of functions that involve the notion of the infinite, we will define each of them in the following sections.

Variable tending to infinity

When a variable tends to infinite, suppose x, we will use the symbol of infinity. This means that the variable x takes arbitrarily large values, in magnitude. Analytically we will say that, fixed a certain real number R, x will exceed it in absolute value, whatever the R taken.

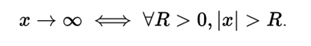
For this definition we will take, as a particular case, two "signs of infinity".

Of special interest is the behavior of certain functions at infinity. When these limits exist, and they are real numbers, we can construct the equation of the horizontal or oblique asymptotes of the function. We will define then the limit of a function, when the independent variable tends to infinity, for any sign.

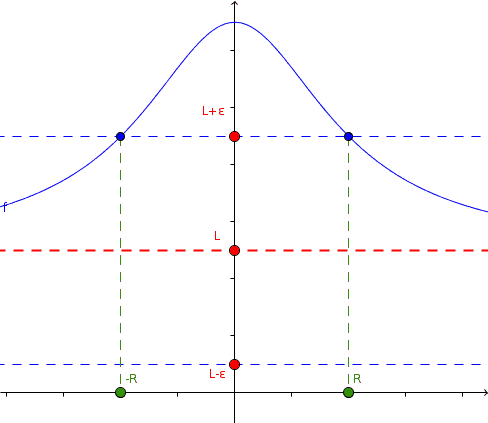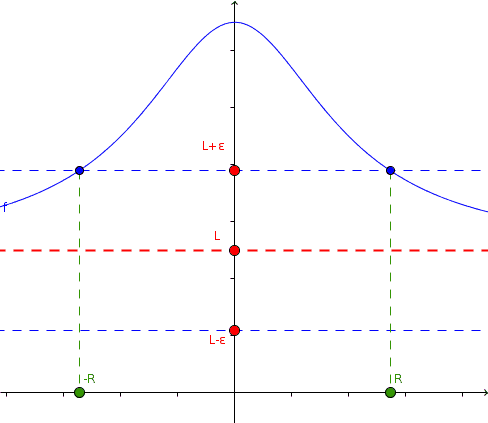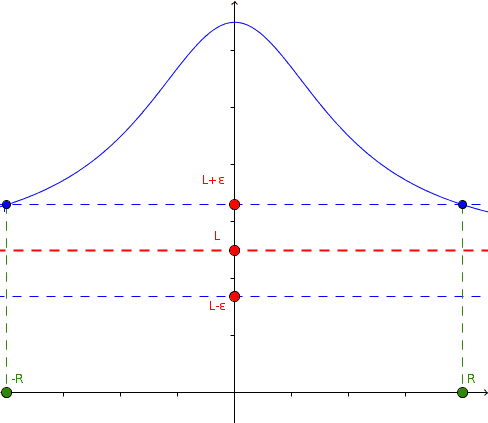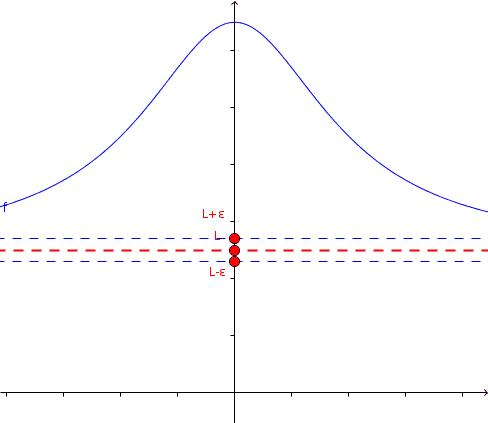
Given ε, R can be established so that f (x) "approaches" L, as x moves away from the origin unlimitedly.

Function that tends to infinity

Given a certain function f, we will say that it tends to infinity when it grows indefinitely, as we approach a certain point c in the domain. This is equivalent to stating that f is not bounded, for values of the domain "close enough" to c.

If we take the function f as a variable, for example, y, we can use the definition of variable that tends to infinity, and combine it with the definition of limit, in the following way.

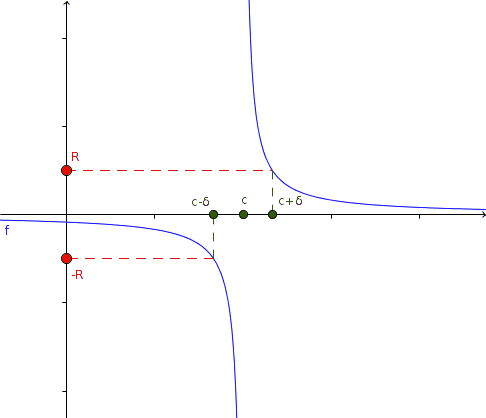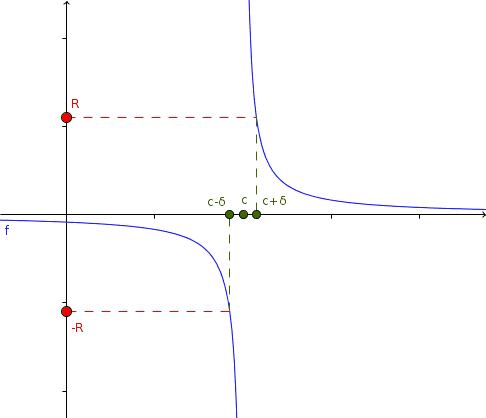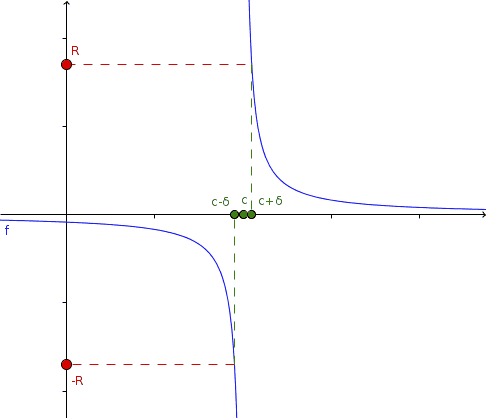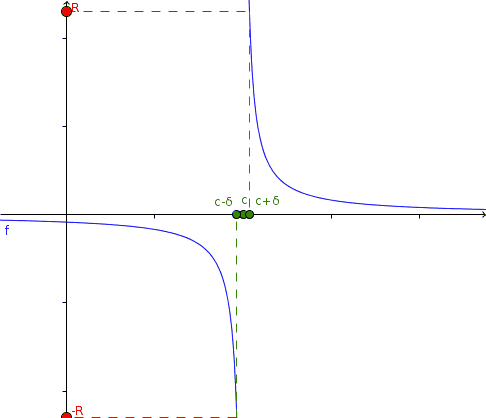
Taking R arbitrarily large, we can establish a δ so that when x approaches c, f (x) exceeds R in absolute value.

Calculation of limits

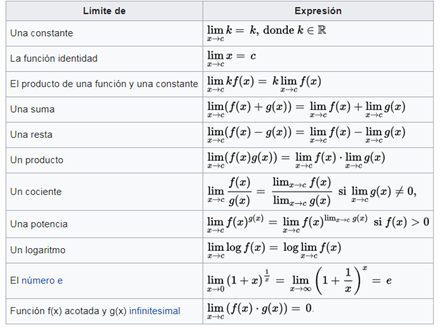
The defined concepts allow to introduce tools for the calculation of limits. From the definitions, algebraic properties can be demonstrated, listed in detail below.

General properties

If f (x) and g (x) are real variable functions and k is a scalar, then the following properties are fulfilled

Regla de l'Hôpital

This rule makes use of the derivative and has a conditional use. This can only be used directly in limits that are "equal" to 0/0 or a ± ∞ / ± ∞. Other indeterminate forms require some algebraic manipulation, usually establishing that the limit is equal to y, taking the natural logarithm in both members, and then applying the l'Hôpital rule.

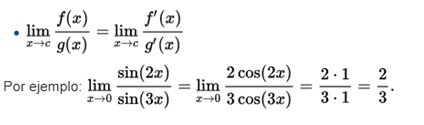
Trigonometric limits

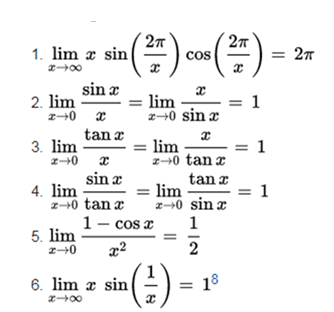
References

1 . Piskunov, N. (1977). Differential and integral calculus (3rd edition). Mir. p. 28. "The concept of the limit of the variable will play a fundamental role, since the fundamental concepts of mathematical analysis are related to it: derived, integral, etc."
2 . MacTutor History of Bolzano
3 . Jump to: a b Jeff Miller's history of math website.
4 . MacTutor History of Weierstrass.
5 . V.F. Butúzov. Mathematical analysis in questions and problems. Mir Publishing, Moscow (1989)
6 . Franco, Manuel; Martínez, Fransisco; Molina, Roque (1995). Lessons of infinitesimal calculation II. EDITUM. pp. 9-10.
7 . Kolmogorov, Andrei (1978). «Metric and topological spaces». Elements of functional theory and functional analysis (3 edition). Moscow: Mir.
8 . Berman and others. Problems of mathematical analysis. Mir, Moscow.