Mathematical Explanation- First Degree Equation
Hello friends of steemit, referring to my publications on mathematics and its properties, today I want to talk about the equation of first degree or linear equation, it is important that in education is investigated in depth and that is why today we will talk about which are the equations that apply this property, as it applies, and I will also show some examples of how to apply the first-degree equation.
Equation of first degree
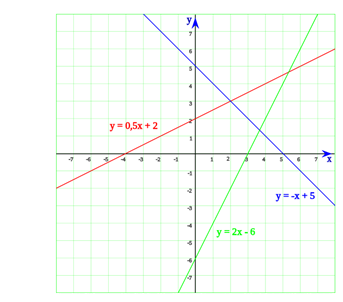
graphic example of linear equations
A first degree equation or linear equation is an equality that involves one or more variables at the first power and does not contain products among the variables, that is, an equation that involves only addition and subtraction of a variable to the first power. In every commutative ring, first-degree equations can be defined.
In an unknown
An equation of one variable mx + n = 0 defined on a body K, that is,  where x is the variable, admits the following solution:
where x is the variable, admits the following solution:
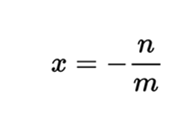
When both the unknown and the coefficients are elements of a ring that is not a body, the procedure is more complicated since there will only be solutions when m divide n:
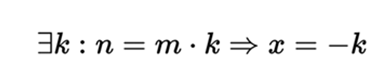
In two unknowns
In the Cartesian system they represent lines, a common form of the linear equations of two variables is:
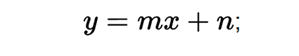
Where m represents the slope and the value of n determines the point where the line intersects the y axis (the ordinate to the origin).
Some examples of linear equations:
Alternative forms
Complex forms like the previous ones can be written using the rules of elementary algebra in simpler ways. Capital letters represent constants, while x and y are variables.
General equation
Here A and B are not both zero. It represents a line in the Cartesian. It is possible to find the values where x and y cancel each other.
Segment or symmetric equation
Here both E and F can not be zero. The graph of this equation cuts the x-axis and the y-axis in E and F respectively.
Parametric shape
Two equations that must be fulfilled simultaneously, each in the variable t. It can be converted to the general form by clearing t in both equations and matching. In this representation it can be affirmed that the line passes through the point(x ,y) and forms with the abscissa axis an angle whose tangent satisfies: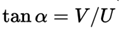
Special cases
A special case is the standard form where A = 0 and B = 1. The graph is a horizontal line without intersection with the x-axis or (if F = 0) concidente with that axis.

Another special case of the general form where A = 1 and B = 0. The graph is a vertical line, intercepting the X axis in E.
In this case, all the variables were canceled, leaving an equation that is true in all cases. The original form (not one as trivial as that of the example), is called identity. The graph is the whole Cartesian plane, since it is satisfied by every pair of real numbers x and y.
Note that if the algebraic manipulation leads to an equation like 1 = 0 then the original is called inconsistent, that is, it is not fulfilled for any pair of numbers x and y. An example could be:
Additionally there could be more than two variables, in simultaneous equations.
Linear equation in n-dimensional space
The linear equations of several variables admit geometric interpretations, when the coefficients of the equations belong to a body. Thus a linear function of two variables of the form:
represents a line in a plane. In several variables assuming that both the variables xi and K and the coefficients xi and K where, K is a body then a linear equation like the following:
represents a hyperplane of n-1 dimensions in the n-dimensional vector space K.
Systems of linear equations
Systems of linear equations express several linear equations simultaneously and admit a matrix treatment. For its resolution there must be as many equations as there are unknowns and the determinant of the matrix must be real and not null. Geometrically correspond to intersections of lines in a single point (linear system of two equations with two unknowns), planes in a line (two linear equations of three unknowns) or a single point (three linear equations of three unknowns). The cases in which the determinant of the matrix is null do not have a solution.
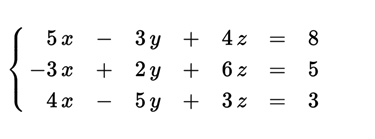
If we consider n linearly independent first degree equations defined on a body then there is a single solution for the system if the conditions of the Rouché-Frobenius theorem are given, which can be calculated by the Cramer rule that is applicable to any body. If the equations are not linearly independent or the conditions of the theorem are not given, the situation is more complicated. If the system is posed on a commutative ring that is not a body, the existence of solutions is also more complex.
Linearity
A defined function on a vector space is linear if and only if the following proposition is fulfilled:
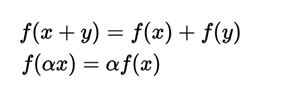
where α is any scalar. It is also called a linear operator f.
Bibliography:
Weisstein,Eric W < Linear Equation >. In Weisstein, Eric w. MathWorld (in ingles).Wolfram Research.
Example of exercises applying the first degree equation.

@joseferrer

@joseferrer
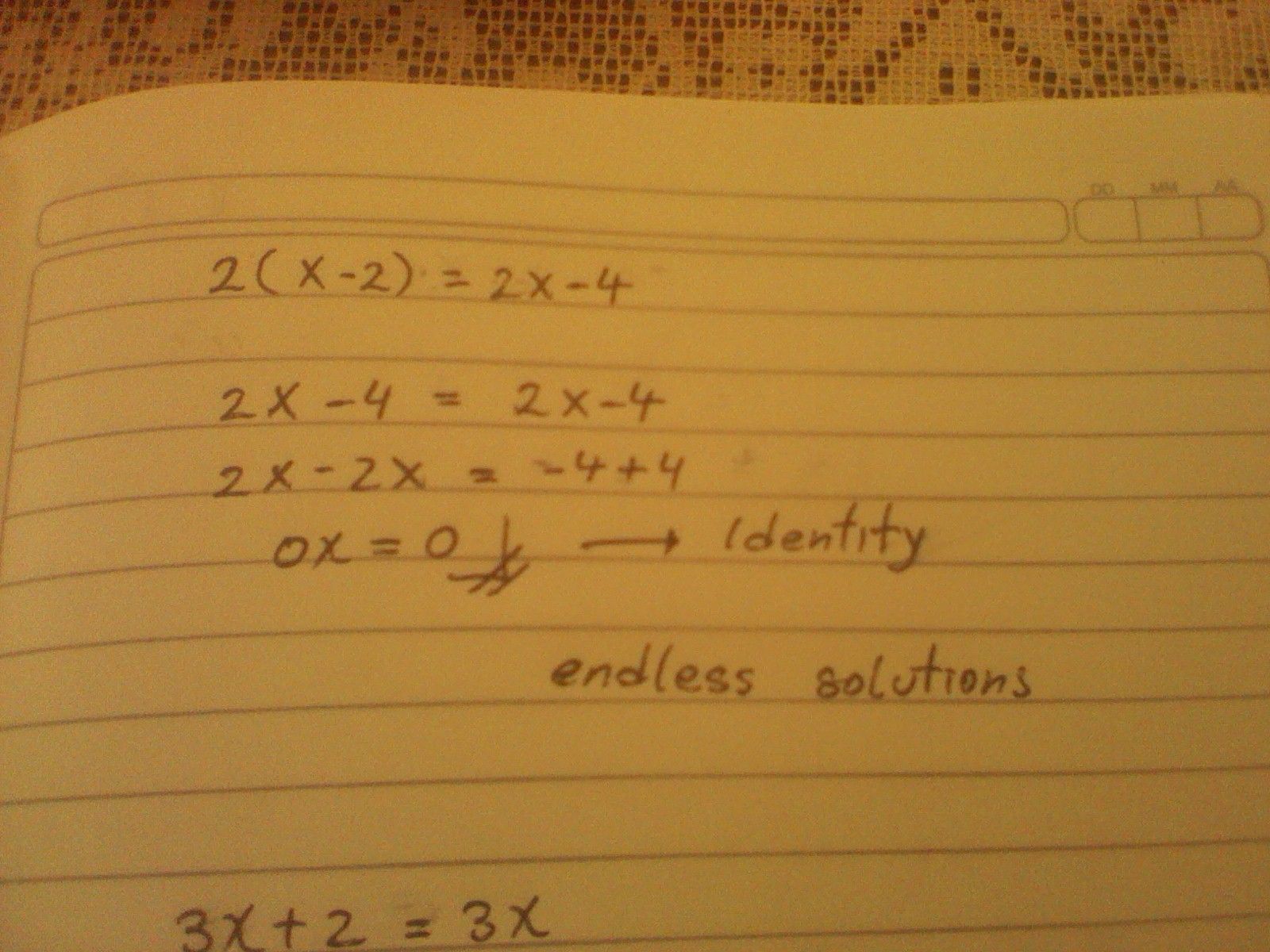
@joseferrer
 @joseferrer
@joseferrer
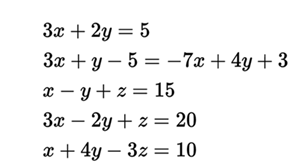
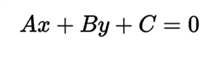


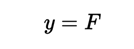
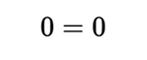
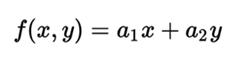
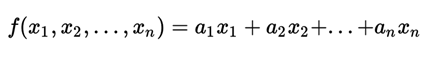
I have learnt a lot from this....i have been searching for tutorials on mathematics, am glad I found out.i have followed you and I would appreciate a follow back.
thank you friend for your comment soon I will be publishing more tutorials on math, thanks for following me and I follow you.