Quadratic Equation (Part 1)

Hello Guys 😁, Welcome to the First Edition Of Learning Mathematics With Hardaeborla. This great Initiative is to share my Mathematical knowledge with everyone on Steemit by taking you through series of Mathematical Tutorials and you may also have the chance of winning SBD for solving my tutorial questions 😁. I hope I get supports from those who believe in improving Educational Standard And Sharing Beneficial Knowledge. Now let's get down to Business 😊.

Quadratic Equation

ax² +bx +c =0

Quadratic Equation is any form of equation in which the highest power of the variable is 2. In the above equation, it is observed that the maximum power of x is always 2. This literally means you are expected to get two solutions after solving every Quadratic Equation.
From my research and studies, I noticed the "Maximum power of the variable of linearly arranged equation determines the number of solutions". This is explained below;

x+b=0=>No of Solution =1

ax² + bx +c=0=>No of solution =2

ax³ +bx² +cx +d=0=>No of Solution =3

If we continue this equation till quartic equations, you will always notice your number of solutions will be equal to the highest power of x. This literally means that Every Quadratic Equation is mostly characterised by the highest power of their variables (x). The general form of every Quadratic Equation is always given by

ax² +bx +c =0
where a, b and c are numbers or constant and a≠0. If a is equal to 0,then we have a new equation known as "Linear Equation". Let's proof the above statement 😊.

ax² +bx +c =0

Put a=0

(0)x² + bx +c =0

bx +c=0

If the graph of bx+c is plotted, it is observed to form a straight line graph with a particular solution after solving which makes it a "Linear Equation". This connotes that for every Quadratic Equation, the coefficient of the highest power which is 2 must never be 0, so that we won't end up getting a Linear Equation.

Solutions To Quadratic Equation

I stated earlier that the number of solutions for every Quadratic Equation is always 2. The values must not be more than 2 after solving Quadratic Equation. In Mathematics, there are 3 popular values after solving any Mathematical Equation. This are

• Complex Numbers
• Rational Numbers
• Irrational Numbers
• Real Numbers

Since Every Quadratic Equation always have two solutions, this means we can either have the following sets of values listed below;

• Real Root Twice
• Rational Root Twice
• Complex Root Twice
• Irrational Root Twice
• Complex and Real Root
• Rational and Irrational Root
• Real and Complex Root
• Irrational and Complex Root

This implies that one shouldn't get astonished or confused if you end up with two distinct roots or real roots. You just have to be sure of what you have done and solve properly by following the required steps.

Methods Of Solving Quadratic Equation

There are four different methods of solving Quadratic Equation. I will try as much as possible to take you through the steps. I hope you will find it very easy to tackle problems dealing with Quadratic Equation. This following method is used to determine the roots of a Quadratic Equation.

• Formula Method
• Completing The Square Method
• Factorization Method
• Graphical Method

Let's now take each method by explaining the concept and applying them to solving Quadratic Equation😊

The Quadratic Formula

The Quadratic Formula is an easier method of determining solutions to Quadratic Equation. Some people in some parts of Countries like Nigeria do call it "Almighty Formula"😀. They had to ascribe such name to it due to it's fast support and easy approach in determining Quadratic Root. This formula came into existence with the perfect work of great Mathematicians done for the past 100 years. This great men include

• Brahamangupta [Indian Mathematician]
• Al Kwarizmi [Arab Mathematician]
• Diophantus [Greek Mathematician]

Deriving The Quadratic Formula

The Quadratic Formula was derived by "Completing The Square Method". I will explain the step by step method of deriving this great formula for the purpose of proper comprehension and understanding to everyone reading this post. Let's Begin 😀

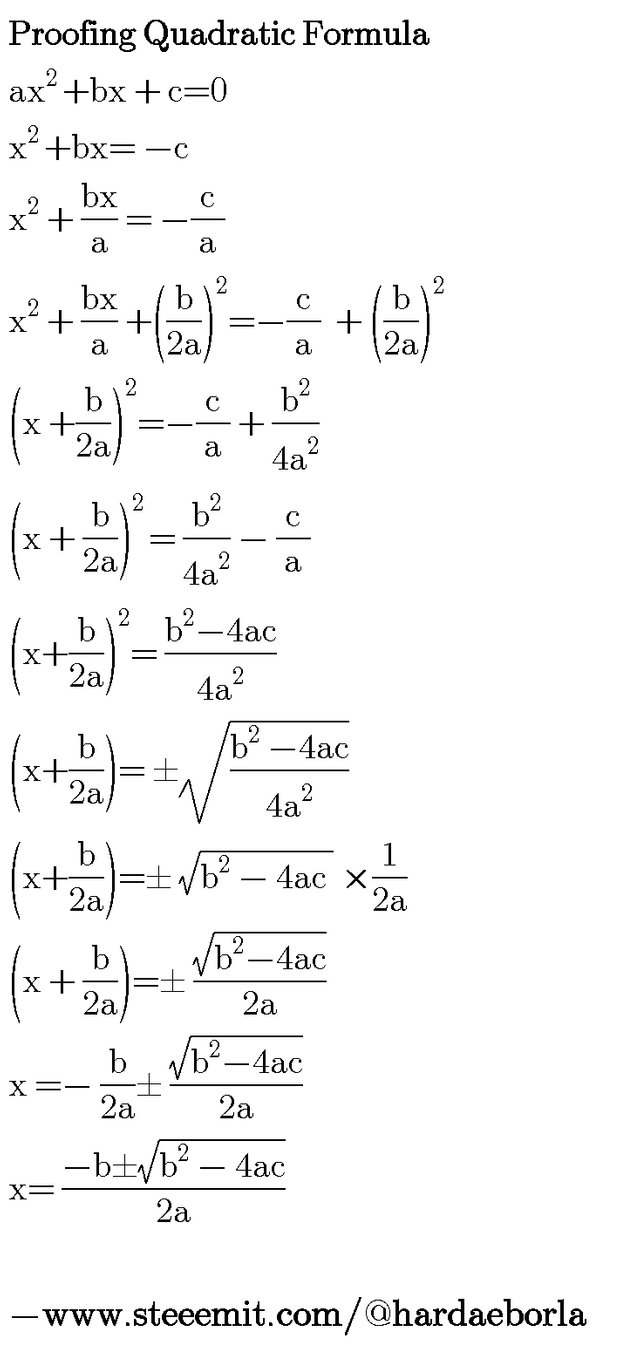
ax² +bx +c =0

That's the general form of Quadratic Equation.

Move "c" to the RHS, Remember there will be a change in sign after crossing the equality sign. We now have;

ax² +bx = -c

Divide both sides by "a"

ax²/a +bx/a =-c/a

x² +bx/a =-c/a

Add the square of half of the Coefficient of x which is (b/2a)² to both sides. We now have

x² +(b/a)x +(b/2a)² =-c/a +(b/2a)²

Simplify the LHS, We have ;

(x+b/2a)² = - c/a +(b/2a)²

Simplify the RHS and find the LCM

(x+b/2a)² =-c/a +b²/4a²

(x+b/2a)² =b²/4a² - c/a

LCM=4a²

(x+b/2a)² =(b² - 4ac)/4a²

Take the Square Root of the LHS

(x+b/2a)=±√[(b²-4ac)/4a²]

The Denominator changed from 4a² to 2a by applying the "law of Indices"

(x+b/2a)=±√(b²-4ac)/2a

Making x the subject of formula, we now have ;

x=-b/2a±√(b²-4ac)/2a

Taking the LCM which is 2a,we have ;

x=-b±√(b²-4ac)/2a

I will stop here for now because it's not easy typing with this faulty phone and I don't have a computer system for now. I hope to buy a new phone or system after gaining more money on Steemit

Feel free to ask questions about what you don't understand, suggestions, criticism and comments is allowed. Stay blessed and have a lovely time 😊🙌.
@steemiteducation,@steemstem,
@surpassinggoogle in courtesy of #ulog. Let's promote Educational Standard On Steemit Platform.