Image source

When children understand that fractions can have different names, they should be challenged to develop a method for finding equivalent names. It might also be argued that students who are experienced at looking for patterns and developing schemes for doing things can invent an algorithm for equivalent fractions without further assistance. However, the following approach will certainly improve the chances of that happening. 

An Area Model Approach 

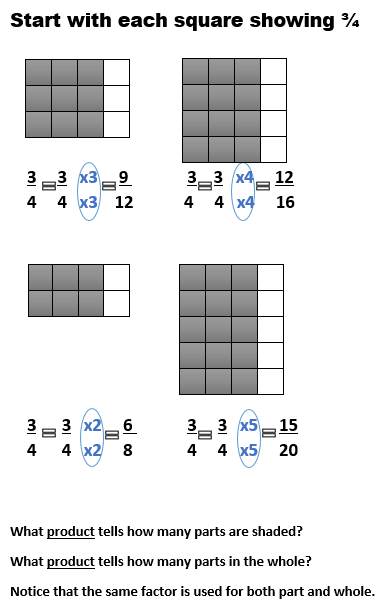
Your goal is to help students see that if they multiply both the top and bottom numbers by the same number, they will always get an equivalent fraction. The approach suggested here is to look for a pattern in the way that the fractional parts in both the part as well as the whole are counted. The following activity is a good beginning, but a good class discussion following the activity will also be required: 

Give students a worksheet with four squares in a row, each approximately 3 cm on a side. Have them shade in the same fraction in each square using vertical dividing lines. For example, slice each square in fourths and shade three-fourths as shown below. Next, tell students to slice each square into an equal number of horizontal slices. For each sliced square, they should write an equation showing the equivalent fraction. Have them examine their four equations and the drawings and challenge them to discover any patterns in what they have done. You may want them to repeat this with four more squares and a different fraction.  

Following this activity, write on the board the equations for four or five different fraction names found by the students. Discuss any patterns they found. To focus the discussion, show on the overhead a square illustrating  ⅘ made with vertical slices. 

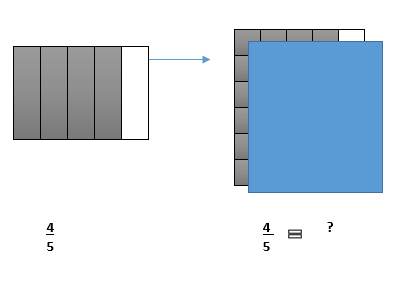
Turn off the overhead and slice the square into six parts in the opposite direction. Cover all but two edges of the square and ask: “What is the new name for my ⅘ ?”  

The reason for this exercise is that many students simply count the small regions and never think to use multiplication. With the covered square, students can see that there are four columns and six rows to the shaded part, so there must be 4 x 6 parts shaded.  

Using this idea, have students return to the fractions on their worksheet to see if the pattern works for others fractions.