Mathematics - Mathematical Analysis Special Sequences and Divergence

    Hello its a me again. Today we continue with Mathematical Analysis getting into some Special Sequences and also more things about the Divergence of Sequences. You should check out my previous post about Subsequences and Convergence here before getting into this post! So, without further do, let's get started!

Bernoulli's inequality:

Suppose x that is a real number and > -1 and also n that is a natural number then:

(1 + x)^n >= 1 + n*x

Using this "equation" we can find the limit of an geometric sequence.

Geometric Sequence:

    A sequence (an) with generic term a(n) = r^n, where n a natural number and r a real number is called a geometric sequence. 

If |r| < 1 then this sequence is also a null sequence and so:

lim n-> +∞ [r^n] = 0.

If r equals 0 then the limit equals 1 and if |r| is greater than 0 then the limit equals +-∞ .

Try proving it using Bernoulli's Inequality. 

    Just suppose a real number x and set |r| = 1 / (1 + x) and try forming the inequality so that you end up with a limit that gives 0.

D'Alembert Convergence/Divergence Theorem:

Suppose a sequence (an) with positive terms and the limit:

lim n->∞ [a(n+1)/a(n)] = l, a real number.

• If 0 < a(n+1)/a(n) < l < 1 then the sequence (an) is a null sequence and so lim n->∞ (an) = 0
• If a(n+1)/a(n) > l > 1 then the sequence (an) diverges and so lim n->∞ (an) = ∞

Example:

Calculate the limit:

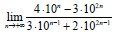
Suppose the limit is an sequence (an) then:

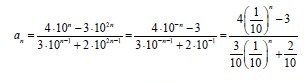
lim n-> ∞ (1/10)^n equals 0, cause 0 < 1/10 < 1 (from D'Alembert) and so:

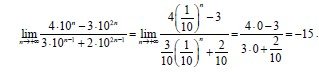
Root Sequence:

    Suppose a sequence (an) with generic term a(n) = n-root(a) for every natural n and a positive real number 'a' then the limit:

lim n-> ∞ [n-root(a)] = 1.

• If a = 1 then we can directly see that it equals 2
• If a>1 then this can be proven easily using Bernoulli's Inequality and the Squeeze Theorem.

So, we can generalize saying that:

lim n-> ∞ [n-root(n)] = 1 for every natural number n > 2.

Napier's (Euler's) constant e:

    We are all familiar with the number e = 2.718... But did you know that this value is actually the result of a sequence's limit?

     So, if you take the sequence (an) with generic term a(n) = (1 + 1/n)^n, a sequence that is strictly increasing, bounded and converging and find the limit of this sequence you will end up with:

lim n->∞ (1 + 1/n)^n = e, where e is the napier constant e = 2.71828....

This can again be proven by using Bernoulli's Inequality.

    We can also calculate it using a Series, something that we will start talking about from the next post on. So, for you to get an idea the series "1+ 1/2! + 1/3! + ... + 1/n!" also gives us 'e', but much faster and so we can use a smaller 'n' value (cause infinity is not feasible) and get a value closer to the 'e' constant.

The sequence (an) with generic term a(n) = (1 + a/n)^n has a limit equal to e^a and so:

lim n->∞ (1 + a/n)^n = e^a

Sum up in form of a table:

The table also contains some other useful limits that may come handy.

Divergence:

    We already said that a sequence diverges when the limit equals to +-∞. But, we don't covered why they are useful and which other properties they have.

Properties of Divergent Sequences:

• A increasing and non-bounded sequence diverges to +∞
• A decreasing and non-bounded sequence diverges to -∞
• A sequence that is not upper-bounded is build up of at least one subsequence that diverges to +∞
• A sequence that is not lower-bounded is build up of at least one subsequence that diverges to -∞
• If (an), (bn) are sequences with a(n) <= b(n) for every natural number n and lim n->∞ (an) = +-∞ (an diverges) then lim n->∞ (bn) = +-∞ and so (bn) also diverges.
• If (an), (bn), (cn) are sequences with b(n) <= a(n) <= c(n) and the (bn), (cn) diverge which means that lim n->∞ (bn) = lim n->∞ (cn) = +-∞ then (an) also diverges and so lim n->∞ (an) = +-∞

    Also, remember the indeterminate forms of limits ∞/∞ and ∞-∞, cause if you end up with something like that you will have to use the tips and tricks we already talked about to get an solvable form.

Example:

Suppose we want to calculate the limit:

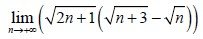
We can clearly see that we have a indeterminate form ∞-∞.

This means that we will use conjugate multiplication and so:

     The limits of 1/n and 3/n to infinity of course give us 0 and that's why we end up with simpler calculations. I think that I don't have to explain more than that.

And this is actually it for today and I hope you learned something!

Next time we will get started with Series and their Convergence!

Bye!