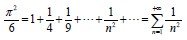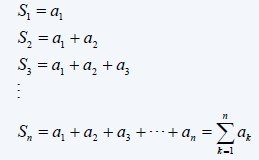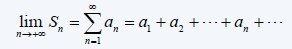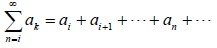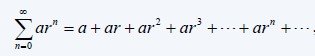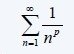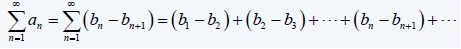Mathematics - Mathematical Analysis Series Basics
Hello it's a me again drifter1! Today we continue with yet another post about Mathematical Analysis getting into Series. I will talk about some Basics to get started and we will get into more specific things posts to follow. So, let's get started!
Getting into Series:
You all are familiar with the number π or pi that equals 3,1415.... But how did we end up with that number? How easy is it to get this number out of some Mathematical Equation?
Archimedes a mathematician of ancient Greece did some calculations and said that pi is in between of two rational numbers. 30/71 < pi < 3/7. But this doesn't give us a clear answer, but just speculates where pi is inside of a large numeral range.
A lot of mathematicians followed giving their own definition of pi as some form of Arithmetic Series.
For example Euler defined pi as:
So, defining pi is not easy and we can just approximately find a value of it using terms of a Series.
And this is mostly what Series are all about. They are about calculating the value/limit that a Series converges to when going to infinity! Each term of this Series/Sum can be anything and so a Sequence or many Sequences combined.
Series Definition:
If (an) is a sequence of real numbers then we create a new sequence of real numbers like that:
where S(n) is called the sum of n terms of the sequence (an).
The limit/value that this sum converges to when n is going to infinity (n -> ∞) is called a Series of real numbers. So, a Series is defined as:
where the real numbers a(n) for every natural number n are called the terms of the Series.
The term a(n) is called the generic term of the Series, the same way as in sequences, but here each term is the value of a sequence.
Sometimes a Series may not start from 1, but from i != 1 and then we write the Series as:
A Series with positive terms is called a positive Series and a Series with negative terms a negative Series. A Series with alternating sign is called a alternating Series.
A Series S is bounded when the sum of n-terms (a1 + a2 + .... + an) is also bounded.
Examples:
- The sum of all the natural numbers is a Series S(n) = 1 + 2 + 3 ... + n = n(n+1)/2 and is called a arithmetic Series
- The sum of all the natural numbers squared is a Series S(n) = 1^2 + 2^2 + 3^2 + ... + n^2 = n(n+1)(2n+)/6 and is commonly used in the mathematical induction method
Series Convergence:
- A Series S converges when the limit to infinity is equal to a real number s.
- When the limit is equal to +-∞ then the sequence diverges.
- When the limit is undefined then the sequence "bounces"
- A Series S absolutely converges when the series of absolutes values if the sequence (an) converges to a real number s
Series Examples/Types:
Geometric Series:
A Series of the form:
with a being the first term and r the ratio.
- When |r| < 1 the series converges to s = a / (1-r)
- When r >= 1 the sequences diverges to +-∞
- When r <= -1 the sequence "bounces"
Harmonic (Dirichlet) Series:
A series of the form:
is called a p-harmonic series.
We will get into the convergence next time.
Tylescoping Series:
A series of the form:
where the generic term a(n) is written as a sub of two other terms of another sequence (bn).
To find out if it converges or not we check the convergence of (bn).
And this is actually all I wanted to cover today!
Next time we will get into how we find out if a Series converges or not using the so called Convergence Testing Criteria.
Bye!