Mathematics - Mathematical Analysis Sequence Basics

    Hello it's a me again! Today we continue with Mathematical Analysis getting into some Basics about Sequences. I will first give you a definition and some examples and then we will get into bounded and monotonic sequences. I will leave subsequences and convergence for the next post. So, without further do, let's get started!

Sequence Definition:

    We all have seen sequences and know some things about them. A sequence is actually a special function that we use recursively. The sequence has a definition set that contains only the natural numbers N=1, 2, 3, ..., n. The value of each term and so the domain of range has real values. So, we define a sequence as a function a: N->R that has a independent variable n and so the term a(n) = an. The terman is called the general term. Sometimes the sequence may start from 0 and so the term a0. 

So, a sequence 'a' looks like this: a1, a2, a3, ..., an, ... and we symbolize it as (an).

    Knowing some terms we can then calculate the value of each other term using a recursive function that will either be given to us or that we can find out by ourself.

Examples:

• The natural numbers are also a sequence with a(n) = n and the first term being a1 = 1. This means that the difference between two neighbour-terms in the sequence is d=1.
• The sequence a(n) = (-1)^n has the following terms -1, 1, -1, ..., (-1)^n, (-1)^n+1, ... This means that domain of range contains only the values -1 and 1.
• a(n) = c is a so called constant sequence where each term is equal to c.
• The sequence a(n) = 2n contains the terms 2, 4, 6, ..., 2n, 2n+2, ... and so represents all even numbers.
• The sequence a(n) = 2n-1 contains the terms 1, 3, 5, ..., 2n-1, 2n+1, ... and so represents all odd numbers.
• The sequence a(n) = n^2/4 contains the terms 1/4, 1, 9/4, ..., n^2/4, ... where each term is a positive rational number.
• The Fibonacci sequence is the most known and each term is equal to the sum of the two previous ones and so a(n+2) = a(n+1) + a(n). The terms a1 and a2 are equal to 1 and so the terms of the fibonacci sequence look like this: 1, 1, 2, 3, 5, 8, 13, 21, ... 

Arithmetic Progressions:

    Sequences like the natural number one are called arithmetic progressions and each term has a constant difference to the previous term. So, a arithmetics progression is a sequence that looks like this:

a(n) = a(n-1) + d 

or even

a(n) = a1 + (n-1)*d 

We will get more into them when we talk about Arithmetics Series posts later on.

Equality: Two sequences a and b are equal only when an = bn for every natural number n.

Bounded Sequences:

• A sequence a is upper bounded when there is a real number M so that an <= M for every natural number n. The number M is called the upper bound of a. The minimum of those upper bounds is the so called supremum sup(an).
• A sequence a is lower bounded when there is a real number m so that an >= m for every natural number n. The number m is called the lower bound of a. The maximum of those lower bounds is the so called infimum inf(an).
• A sequence is simply bounded when upper and lower bounded.
• A sequence is absolutely bounded when there is a positive real number a so that |an| <= a. This number a is called the absolute bound of (an).

    A sequence (an) is bounded only when it also is absolutely bounded something that is pretty easy to find out, cause if a sequence is bounded then we can take the absolute maximum of the lower bound m and higher bound M, let's say a = max{|m|, |M|} and so the sequence then is absolutely bounded by the real number a.

Example:

    The sequence an = 1/n contains the terms 1, 1/2, 1/4, 1/8, ... and this makes it clear for us to see that it is upper bounded by M = 1. Also 1/n will get close to 0 and so the sequence is also lower bounded by m = 0. This means that 0 is the infimum and 1 is the supremum of the sequence (an). If we take the max of m and M we see that this max absolutely bounds the sequence an and so |an| < 1

Sequence Monotony:

• A sequence is increasing when a(n) <= a(n+1) for every natural number n
• A sequence is strictly increasing when a(n) < a(n+1) for every natural number n
• A sequence is decreasing when a(n) >= a(n+1) for every natural number n
• A sequence is strictly decreasing when a(n) > a(n+1) for every natural number n
• A sequence is (strictly) monotonic when it is (strictly) decreasing or (strictly) increasing.
• A sequence is constant, when it is increasing and decreasing at the same time. So, an = c for every natural number n.

Other stuff we can now find out:

• A strictly monotonic sequence is also monotonic, but a monotonic is not always strictly monotonic as well.
• A decreasing sequence is upper-bounded and has a upper bound equal to the first term
• A increasing sequence is lower-bounded and has a lower bound equal to the first term
• To find out the monotony we check the quotient a(n+1)/a(n). If the value is greater then 1 then the sequence is strictly increasing, and if the value is less then 1 then the sequence is strictly decreasing. If the value is 0 for at least one natural number n then the sequence is only monotonic. 
• Sometimes its better to check the sign of the difference a(n+1) - a(n) knowing that the sequence is increasing when it is positive and decreasing when it is negative.

Examples:

1. 

Suppose the sequence a(n) = 2n - 1

By setting n = n+1 we get the n+1 term:

a(n+1) = 2(n+1) - 1 = 2n - 1 + 1

The difference a(n+1) - a(n) = 2n -1 + 1 - (2n - 1) = 1 > 0 and so the sequence is increasing.

This means that the function has a lower bound equal to the first term: m = 2*1 - 1 = 1.

 2. 

Suppose the sequence a(n) = (n-1)!/n^n,

where ! is representing the factorial n! = 1*2*...*n. With 0! = 1! = 1

We use the quotient a(n+1) / a(n) and end up with:

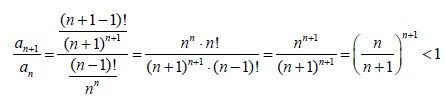
So, the sequence is strictly decreasing and has a upper bound M = (1-1)!/1^1 = 1/1 = 1.

And this is actually it and I hope that you enjoyed it!

Next time we will get into subsequences and convergence!

Bye!