Mathematics - Mathematical Analysis Limit Solving Examples (with roots)
Hello its a me again drifter1! This time we continue with Mathematical Analysis getting into something that I don't covered when we got into Limits. We don't solved more complicated limits that contain roots and this is exactly what I will cover today. So, without further do, let's get started!
Rational with polynomials:
If you remember from previously when the degrees of the denominator and numerator are equal we then know that the limit is equal to the quotient of coefficients of the largest degree of x.
So, for example when having the limit:
We see that if we take x^2 as a common factor then we end up with 1/x that equals 0 and the x^2 quotient gives us 1 and so the result is 1/3.
Rational with Roots:
If we have a rational with roots then we use the so called conjugate multiplication technique. This means that we multiply and divide our limit with the numerator or denominator conjugate.
For example that limit:
You can see that we multiply with root(x) + 2 that is the conjugate of root(x) - 2.
This will now give us a limit that is solvable.
lim x->4 [( x - 4) / (x - 4)*(root(x) + 2)].
You can see that the (x-4)'s give us 1 and so we end up with:
lim x->4 [1/(root(x)+2)] = 1/(2+2) = 1/4.
Try solving the following limit:
You have to get -1/8 as the result.
Polynomial as subroot:
When having a polynomial in the subroot you take x^2 as the common factor. That way x will get out of the root (root(x^2) = x) and the subroot will contain 1/x^n that are all equal to 0. We then also sometimes add and substract x to get a even better form or even take x as a common factor.
For example:
You can see that we take x^2 as a common factor and so get 1/x^n factors in the subroot.
So the limit now gives us
lim x->∞ x*(1 - a) = ∞.
So, if we had the same but also divided by x then we would had 1-a as the result.
Combined cases:
When the limit is rational and also contains polynomial subroots you might have to do both. You will use the common factor x^2, x^4 etc. to get 1/x^n parts in the subroot and then mostly take that as a common factor or create products that will be eliminated with the denominator, that will also need to be made into a product. That way you then end up with simpler polynomial-only cases.
But I think that you mainly will have simple cases that I covered today in you're assignments and tasks in math, cause solving the other cases is much more difficult and takes more time. But, even when you have some other case you will be able to know what to do and it might also turn out easier than you think.
And this is actually it!
I wanted to cover more examples, but I don't have much time today, so yeah I hope that it's enough for you to understand at least the basics! From next time on we will start getting into Sequences and Series!
Bye!
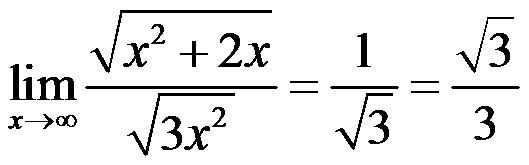
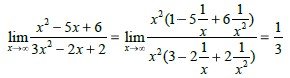
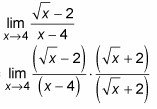
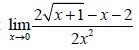
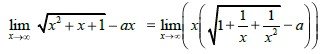
We'd love to see some sources for further reading in this subject! And use our tag!