Mathematics - Mathematical Analysis Integral Applications and Examples
Hello its a me again drifter1! First of all I want to thank you for your support, cause we finally reached 300 followers and it's a sign of appreciation and makes me really happy and gives me the courage to continue posting for you guyz and girlz! Today we will get into some Applications of Integrals that are for calculating the Area of a Plane, the Volume of a solid object in rotation and lastly the length of a curve (actually the one of the function in some specific range)! In the Example of each Application I will use specific Integration Techniques that depend on the Integral and so it would be good to check out my previous posts about them if you find yourself having problems in solving them! So, without further do, let's get started!
Area of a Plane:
We already talked about it when we where talking about Indefinite and Riemann Integrals. To calculate the Plane you use a Riemann (Definite) Integral on the absolute function f (|f(x)|) in an specific range (a, b).
This looks like this:
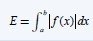
And the interpretation is actually pretty simple. When the function has a positive value we just use the integral in that range. But, if the function has a negative value in some range we then use the "minus" of that so that we finally get the whole Area of the function adding all those subrange-areas with the specific sign.
When having two functions and wanting to calculate the area in between we use a similar concept.
We will get the substraction of f with g, but f will sometimes be under g and so the result will be be negative in those cases and so then we use the "minus" of that again. So, the integral contains the absolute value of f-g and looks like this:
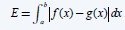
Example:
Let's get into an example for the second type, cause we already did one for the first and the concept is either way the same.
Find the Area between f(x) = 6x - x^2 and g(x) = x^2 - 2x
Solving the linear system of f and g we see that they cut at the points:
A(0, 0) and B(4, 8).
It's simple to find the sign of f-g cause:
6x-x^2 - (x^2 - 2x) = 6x -x^2 -x^2 +2x = -2x^2 +8x.
Because a = -2 and is negative we know that the whole function is >0 only in between of 0 and 4 and so we have to calculate the integral -x^2 + 8x in the range (0, 4) that gives us:
Integral 0->4 (8x - x^2)dx = [4x^2 - 2x^3/3] 0->4 = (4*4^2 - 2*4^3/3) - (0 - 0) = 64 - 128/3 = 64/3.
The function graphs look like this:
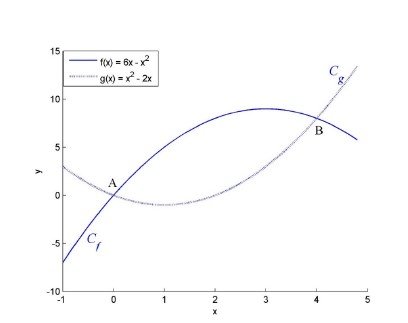
and you can see that the cuts are at A and B that are exactly what we calculated earlier and that the area is the circular thing in between where f is on top of g. Off course we could have g be on top of f at some point, but here we end up with only one area being "real", cause we can't calculate the Area to infinity ( or can we? :P ). Well, we can calculate the rest, but here we only want to check the area of f-g in the range (0, 4) that is drawn by the vertical lines x=0 and x=4.
Volume of a solid object in rotation:
The volume has been proven to be calculated using a specific Integral that contains our function of intereset.
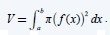
Using this integral where f is always squared we get the volume of the solid that gets formed when f is rotating at the x axis.
With the same concept as before we can also calculate the volume of two functions using:
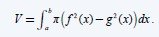
Where we simply get the substraction of f and g having both squared individually!
Example:
Let's only make a simple example for the first type.
Calculate the Volume of y = f(x) = 2 - x^2 when rotated in the range (-1, 1) and so in between of the vertical lines x=-1 and x=1.
When in that range 2 - x^2 is always positive.
We simply have to calculate the integral directly of f^2 and so:
V = π integral -1 -> 1 [(2-x^2)^2 dx].
We know that the integral of -1 -> 0 is equal to the one from 0 -> 1 an so we have to calculate one like that:
2*π integral 0 -> 1 [4-4x^2+x^4 dx] = 2π * [4x - 4x^3/3 + x^5/5] 0->1 = 2π * (4 - 4/3 + 1/5) = 86π/15 .
Length of a (function) curve:
There again is an proven integral for that that looks like this:
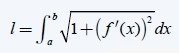
Don't worry about the root so much, we will mostly just set the subroot equal to t using substitution and then just continue on solving!
So, let's get into an Example directly.
Example:
Calculate the length of the curve y = f(x) = x^(3/2) from point (1, 1) to (4, 8).
f'(x) = 3/2 root(x) and so:
l = integral 1 -> 4 [root(1+9x/4)dx]
We set t = 1+ 9x/4 and so dx = 4/9 dt and:
l = 4/9 integral [root(t)dt] = 4/9 * 2/3*t^(3/2) + c = 8/27 * (1+9x/4)^3/2 + c
So, finally we have:
l = [8/27 * (1+9x/4)^3/2 ] 1 -> 4 = 8/27 * (10^3/2 - 13^(3/2)/8) = 8/27 * (10 root(10) - 13root(13)/8).
And this is actually it and I hope you enjoyed it!
Next time I will show you how to solve Limits that contain Roots, something that I forgot to do!
Bye!