Mathematics - Linear Algebra Introduction

Hello my friends I'm back! I was gone for the weekend and didn't had anything prepared and so here we are again. Today we start a new subdivision on this blog. I have a lot more to tell you, but in many things you will need some knowledge of specific mathematical regions. That's why we today start out talking about Mathematics as well, starting off with Linear Algebra! I will only make a quick introduction today and we will see how it goes :) So, without further do let's get started!
Introduction:
Linear Algebra is the branch of mathematics that studies vector spaces and linear mappings between such spaces. So, Linear Algebra starts with vectors and gets even into n-dimensional spaces. But, in our little series we will get into pretty simple stuff. We will first cover Matrix algebra, where we will also talk about methods that help us solve linear equations (getting into determinants at some point). Then we will get into vector spaces, linear functions and lastly eigenvalues and vectors. Today, I will only talk about Matrix algebra basics and also give you an introduction to linear systems, where we will use a method that people may remember from highschool!
Matrix:
A Matrix is an rectangular array of numbers arranged in rows and columns. Each array has a specific size or dimension that represents the number of rows or columns. A matrix with R rows and C Collumns is a RXC array. So, an 4x2 array has 4 rows and 2 columns. Each item has a specific position that is specified by the row and column index its on. So, we are talking about aij items that are in the i-row and j-column, where i<R and j<C that are the number of rows and columns of the matrix. The items with the same index of i and j constitute the main diagonal.
Array-Vector Types:
- When the number of rows and columns is the same than we are talking about a square matrix.
- An array that has only one row is an row vector and an array that has only one column is an column vector.
- When the array has one row and column and so only one item it's called an vector item.
- When the numbers under the main diagonal are all 0 we talk about an upper triangular array, and when the numbers over the main diagonal are 0 we have a lower triangular array.
- An array that is upper and lower triangular and has numbers different to 0 only in the main diagonal is called a diagonal array!
- A diagonal array that has only 1's is called a identity matrix.
- When all the numbers are 0 the array is called a zero-array.
- When inverting the columns with the rows and vise versa we end up with the transpose of an array.
- An array with aij=aji is called symmetrical.
- When matrix A is equal to the negative transpose of A we are talking about an anti-symmetrical array!
Operations:
- Two matrixes are equal when all the items in the corresponding indexes i and j are equal.
- When adding (subtracting) we add the numbers in the same indexes and get a new matrix as result.
- When multiplying with a number (scalar multiplication) we simple multiply each number of the array with the number we are multiplying with.
- When multiplying matrixes the result is more complicated! We can multiply 2 matrixes only when the number of columns of the first one is equal to the number of rows of the second one. For example: A(3x5) * B(5x7) = C(3X7). Each item is equal to a sum: cij = ai1*b1j + ai2b2j + ... + aik*bkj.
So, we can have cases like these:
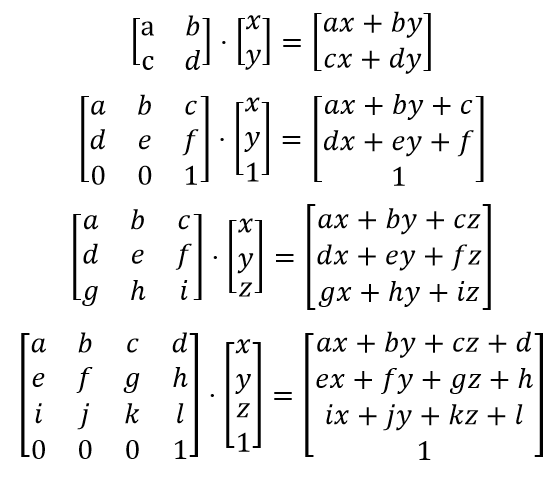
Lastly an important equation has to do with the inverse array that only matrixes that are inversible have. When multiplying a Matrix A with another matrix X the result can become a indicator array I, and when that happens X = inverse A or A^-1. So, A*X = I, when X = A^-1. This equation will become handy next time when we get into Linear Equation solving using the Gauss method!
Linear System Example:
Now let's also lastly get into a simple 2x2 linear systems that many know how to solve from highschool. Suppose we have x+y =5 and x-y =20.
A Linear System is represented like that:
x + 2y = 5
x - y = 20
In highschool we learned a method that simply does multiplication on those equations and additions/substractions between those equations.
For example here we could multiply the second one by 2 and then add them so that we get the value of x, and then simply put the value of x in one of the others to get the value of y.
This looks like this:
x + 2y = 5
x - y = 20 (*2)
-----------------
x + 2y = 5
2*x - 2*y = 40
+
3*x = 45 -> x = 15
x + 2y = 5 -> 15 + 2y = 5 -> 2y = -10 -> y = -5
I hope that you now remember how we solve an linear system and next time we will get into how we solve bigger systems using a matrix method from the mathematician Gauss that uses operations between the rows and columns to form a specific array that then gives us the variable values!
And this is actually it for today! I hope you enjoyed it!
Give me your feedback and get ready for the next mathematic post...Off course I will continue posting programming related stuff, but as I said before in this post, we will need some advanced mathematics later on when we get into more advanced programming stuff and so I thought it would be a great idea to get into a little bit of mathematics beforehand!
Bye!