Sketching Rational Functions in the Cartesian Plane

Note: This topic was requested by a reader from Singapore. If you would like to request a topic, please feel free to suggest one in a comment.

A rational function is a function which is essentially the ratio (hence its name) of two polynomials, i.e. 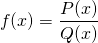, with the caveat that Q(x) cannot be the zero polynomial.

When graphing a rational function, you will need to consider a few things. Most importantly, these are:

1. Intercepts: The places where the function crosses the x or y axis.
2. Asymptotes Asymptotes are lines that the curve of the graph approaches, but never reaches. For most problems in curve sketching, there will be three kinds of asymptotes: vertical, horizontal, and oblique
3. Critical points: If you know differential calculus, you can determine local maxima or minima, as well as inflection points. This will also aid you in knowing on which ranges the graph increases or decreases.

Finding the intercepts in a rational function

• The y-intercept of any function is the value of that function when x = 0, or (x, f(0)), provided of course that the function is defined x = 0.
• The x-intercepts are the zeros of the numerator function, P(x). In other words, they are the places at which P(x) = 0.

Determining the asymptotes

For some reason, many people find this a bit hard, but in reality, there are only a few rules. First we consider the degree of both P(x) and Q(x). I will denote them here as deg(P) and deg(Q), respectively.

• A vertical asymptote exists at x = a, if and only if Q(a) = 0, and .
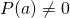
• If deg(P) < deg(Q), then the denominator gets faster much quicker than the numerator, so there will be a horizontal asymptote at y = 0
• If deg(P) = deg(Q), then the denominator gets faster much quicker than the numerator, so there will be a horizontal asymptote at y = a/b, where a and b are the leading coefficients of P(x) and Q(x)
• If deg(P) = deg(Q) + 1, then there is an oblique asymptote. You must find the asymptote by polynomial long division.

Note that if P(x) = Q(x) = 0, you have a removable discontinuity or a "hole". A hole is simply a break in the graph, and the function is undefined at that point, since 0/0 is undefined.

Graphing your function

In general, you should try and find your intercepts and asymptotes first. You can plot the intercepts, and then use dotted lines to represent the asymptotes. Note that the asymptotes are not actually part of the function itself, but rather serve as "guides" that will influence the shape of the graph.

Suppose we wish to graph .

Step 1: Find the intercepts. f(0) = 1.5, so the y-intercept is (0,1.5).

Factoring the numerator gives (x+3)(x-1), so the intercepts are at (-3, 0) and (1, 0). Plot these points on the plane like this:

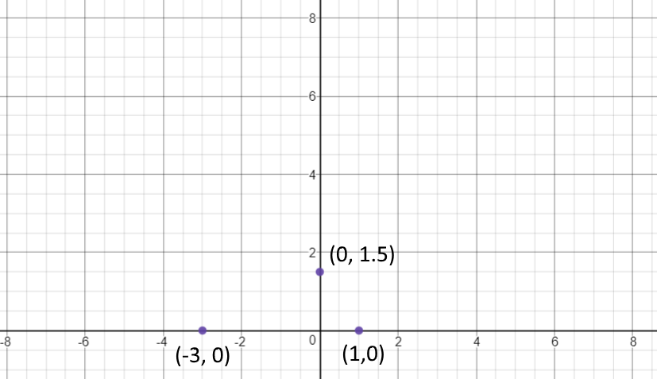
image created using desmos.com

Step 2: Find the asympotes. In this case, there is an asymptote at x = 2. Also, since the P(x) is quadratic, and Q(x) is linear, there is an oblique asymptote. Dividing the polynomials gives x + 4 with a remainder of 5, so the oblique asymptote is x + 4. Therefore, we add x = 2 and y = x + 4 to the graph.

Image created by desmos.com

Finally, we can start to plot. We know the graph must contain the points (-3, 0) and (1, 0) and (0, 1.5). Clearly, there won't be a branch in the region x < 2 and y > x + 4, because then the graph would cease to be a function. So, does the second branch exist in x > 2 and y < x + 4 or x > 2 and y > x + 4? We can find this out merely by picking any value that is greater than x =2 and plugging it into f(x). For instance f(3) = 12, so we add (3,12) to the graph to find out it exists in the region x > 2 and y > x + 4. We can add other points as well. For instance f(4) = 10.5, so I'll add the point (4, 10.5) as well. I can connect the points, and the final product looks like this:

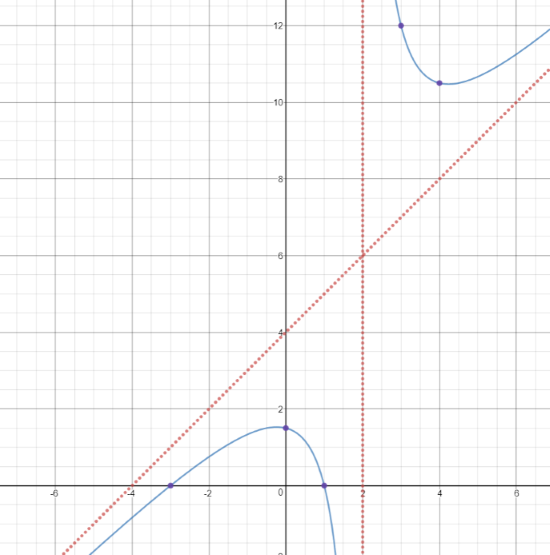
graph created by desmos.com

Concluding remarks

To graph a rational function, you should first find the intercepts and the asymptotes. Use the asymptotes to divide up the plane into different regions, which you can then use to deduce where the graph should be drawn. If you're not sure, you can simply pick values for x to deduce what the graph should look like. Remember, the graph approaches the oblique or horizontal asymptotes as it x approaches positive or negative infinity, but will never touch it. Also, the function is not defined at vertical asymptotes so the graph also does not cross these lines.