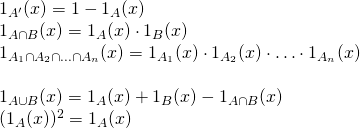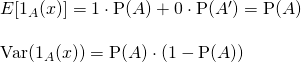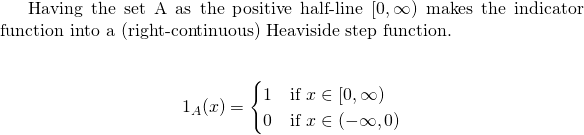The Indicator Function
Hi there, this post will be about the indicator function. I was introduced to this topic informally by a former theoretical physicist who later got into financial mathematics and taught us probability theory. The contents here is based from my old notes, my memory and a part from this book.
It is assumed that the reader is familiar with basic probability theory and basic set theory.
A more longer and more technical version of this post is from my website here.
The math text and images rendered with QuickLaTeX.com.

Definition
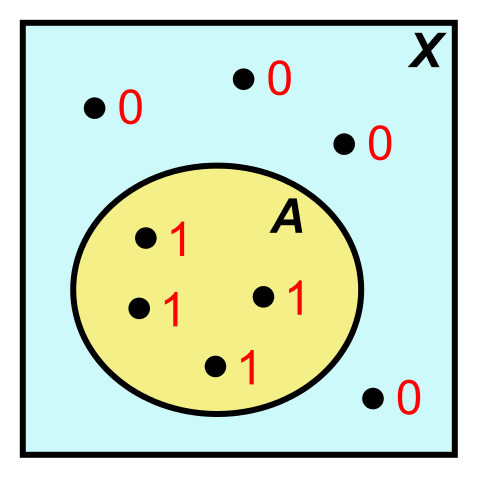
Properties
Some basic properties of the indicator function are based from set theory. The set A' is the complement of the set A, A∩B is the intersection of the sets A and B, and A∪B is the union of the two sets A and B.
Since the indicator function is a random variable, we can find the expected value and the variance of it. The P(A) notation stands for the probability of outcomes in set A occurring.
Heaviside Step Function Example
Changing Integral Bounds Examples
Note that the integral at a single point is zero (area of a point is zero). There is no difference in using an open interval or closed interval.