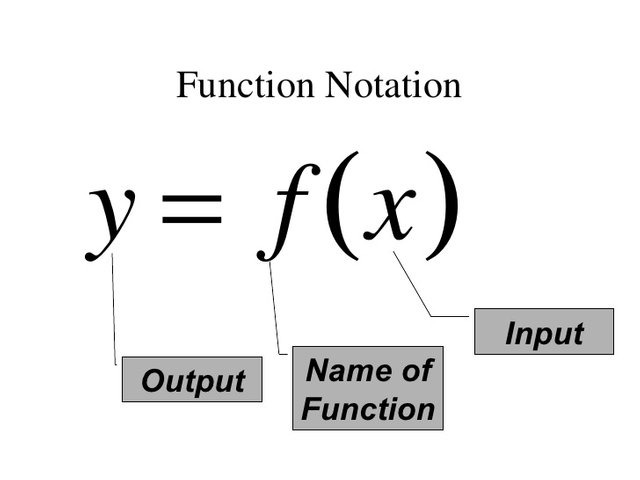
Function Notation
Hi there. This post is an introduction to function notation from (high-school) mathematics.
When it comes to equations, the variable y is commonly used to represent the dependent variable with x being the independent variable. There are times when we deal with multiple equations such as:
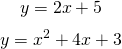
With those equations, when we substitute a value of 2 for x for example it is not entirely clear which y equation we put x = 2 into.
One solution is to use subscripts such as 
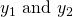
. A more common approach is the use of function notation such as f(x) and g(x). (You can combine subscripts and function notation too!)
Function notation makes it easier for the math reader to identify which equation is being used for the substitution. Instead of y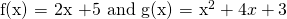, we would use use 
instead. (Different letters are used to indicate the functions are different.)
For the case of substituting x = 2, we have f(2) and g(2) as follows:
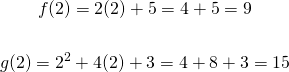
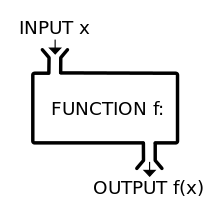
As a summary, here is an informative image. The independent variable x is the input while y = f(x) is the output from x. Think of functions like a vending machine.
Examples
For the first three examples we have h(x) = 10x + 3.
Example One
What is h(1)?
We have h(1) as 13.
Example Two
What is h(-2)?
Example Three
What is h(a) where a is some number?
In the previous examples, the variable x was replaced with a number. Here we do a similar procedure and substitute x with a.
Example Four
Function notation can be applied to more complex functions.
Example Five (Composition Functions)
This example is a little bit tougher. You can have functions inside functions.
Answer
When it comes to composition functions, you start with the inside. For f(g(2)), you evaluate g(2) first and use the value from g(2) into the function f.
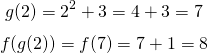
With g(f(2)), f(2) is evaluated first and the value from that is put into the function g(x).
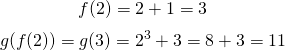
The answers are f(g(2)) = 8 and g(f(2)) = 11.
Math text and images are done in LaTeX with QuickLaTeX.com.
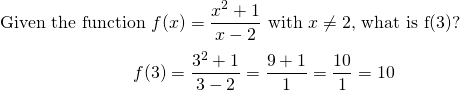
Beautiful lecture, @dkmathstats. I remember my secondary school days. Simultaneous equations was my favourite. I hope I can teach it here, lol. @greatness96
Congratulations @dkmathstats, this post is the ninth most rewarded post (based on pending payouts) in the last 12 hours written by a User account holder (accounts that hold between 0.1 and 1.0 Mega Vests). The total number of posts by User account holders during this period was 2082 and the total pending payments to posts in this category was $2133.89. To see the full list of highest paid posts across all accounts categories, click here.
If you do not wish to receive these messages in future, please reply stop to this comment.