A Math & Finance Introduction To Compound Interest

Image Link: https://pixabay.com/en/money-coin-investment-business-2724241/
Hello. This is my brief take on compound interest from the mathematics perspective. The pictures are from their respective online sources, a few of them are from my camera phone and some of the images are screenshots from RMarkdown.
Disclaimer
This information is based on what I know about finance based on what I have learned from financial mathematics courses. Manage your money and funds at your own risk.
Table of Contents
- What Is Compound Interest?
- The General Formula
- The Impact of Compound Interest
- Examples Of Financial Products Which Use Compound Interest
- Non-Annual Interest Rates
- References
What Is Compound Interest?
Before we define compound interest, we look at a couple of definitions.
Principal - The initial amount/capital being borrowed in a loan or invested into a financial account.
Interest - A compensation amount that the borrower pays the lender for borrowing the principal amount. The lender receives this compensation amount from the borrower (The lender wants extra money for letting the borrower use the money).
Interest Rate - A compensation rate/percentage from the principal for the year in which the capital has been invested or borrowed.
Future Value - The value at a later point in time when the principal in the account has been affected by (compound) interest over time.
Example
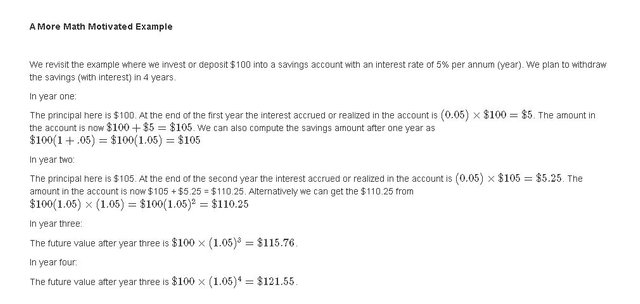
Suppose we invest or deposit $100 into a savings account with an interest rate of 3% per annum (year). We plan to withdraw the savings (with interest) in 3 years.
In year one:
The principal here is $100. At the end of the first year the interest accrued or realized in the account is (0.03) x $ 100 = $ 3. The amount in the account is now $100 + $ 3 = $ 103.
The formula is Principal + Accumulated Interest = New Amount
In year two:
The principal here is $103. At the end of the second year the interest accrued or realized in the account is 0.03 x 103 = $ 3.09. The amount in the account is now $103 + $3.09 = $106.29.
In year three:
The principal here at the start of year three is $106.29. At the end of the third year the interest accrued is 0.03 x $106.29 = $3.19. The amount in the account is now $106.29 + $3.19 = $109.48.
We take out our savings with the accrued interest at the end of the third year and receive the future value of $109.48 (with no deductions assumed).
Notice how each the interest at the end of the year is different and is not always $3. These amounts were different because we still had money in the savings account. Leaving the money into the savings reinvests the principal allowing the interest do its work on the "new principal". This reinvestment trait is a main contributor to compound interest.
Compound interest is interest on interest.
Note that compound interest works the same way as above with loans (where you were lent money and have to pay it back with interest).
In the mathematics sense, compound interest is interest on interest and can be expressed with multiplication. Compound interest is based on exponential growth.
A More Math Motivated Example
The General Formula
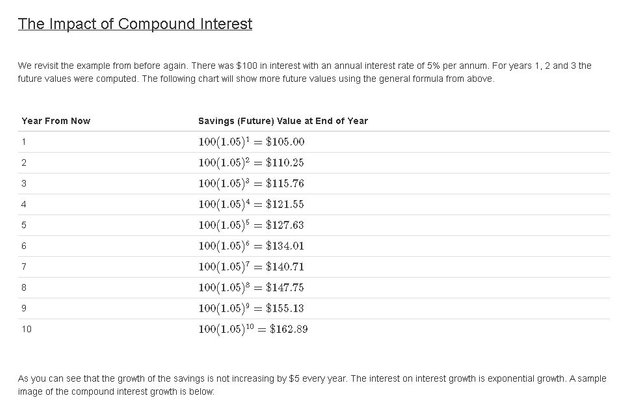
The Impact of Compound Interest
Source: http://moneytipcentral.com/what-is-compound-interest
A higher initial principal gives the account a bit of a "head start" as there is a lot of funds in the account already.
A higher interest rate gives higher growth on the principal and future values.
As more time goes on, the value in the account increases significantly (steepness of curve).
Examples of Financial Products Which Use Compound Interest
In a society which is dependent on finances, many of us deal with financial products which use compound interests. Such products include:
- Registered Education Savings Plans (RESPs) [Common in Canada]
- Bonds
- Credit Card Loans
- Mortgages
- RRSPs for Retirement
- Savings/Chequing Accounts
Non-Annual Interest Rates
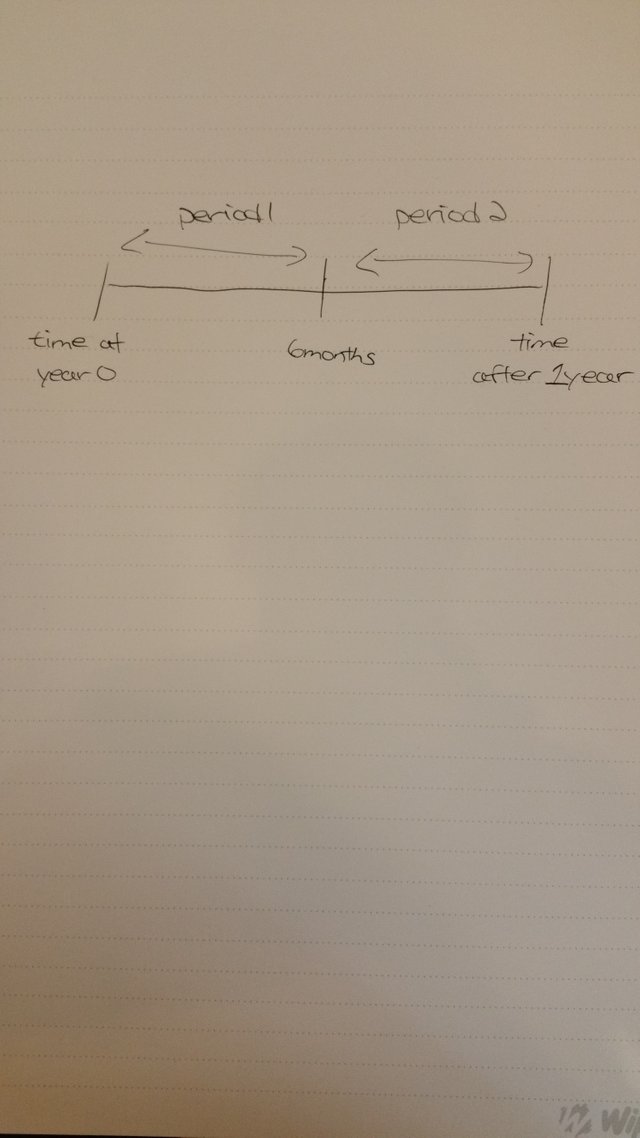
In the previous section, interest rates were on an annual basis. Having non-annual interest rates changes how the interest is compounded in terms of amount and frequency.
If we have a semi-compounded interest rate then we have 2 periods of 6 months each per year. Each interest rate period lasts for six months.
For the quarterly compounded interest rate (compounded 4 times a year) then we have 4 periods of 3 months each per year. Each interest rate period lasts for three months.
For the interest rate being compounded monthly (compounded 12 times a year) then we have 12 periods of 1 month each per year. Each interest rate period lasts for one month.
Examples
References
The featured image is from https://pixabay.com/en/money-coin-investment-business-2724241/.
Book Reference Financial Mathematics: A Comprehensive Treatment by Giuseppe Campolieti and Roman N. Makarov


This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @dkmathstats!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Good work there.
Some of your images seem to come without a copy-right license. The photos you took are fine but if you take an image from a website which does not explicitely state that the image can be used for re-use (in a commercial sense) then you cannot use it. It is unfortunately just how things work.
Fixed. Changed first image and removed the simple/compound interest image.
Good job