Fun Proof of @kenchung Math Competition #4

Problem stated here.

The following map shows the location of three cities A, B and C. The black lines represent roads. Ken wants to travel from A to C, subject to the following rules:

• In each move, he travels from one junction to another junction via the roads.
• Throughout the whole journey, he only moves towards the North or the East, but not any other directions.
• He needs to pass through B.
  

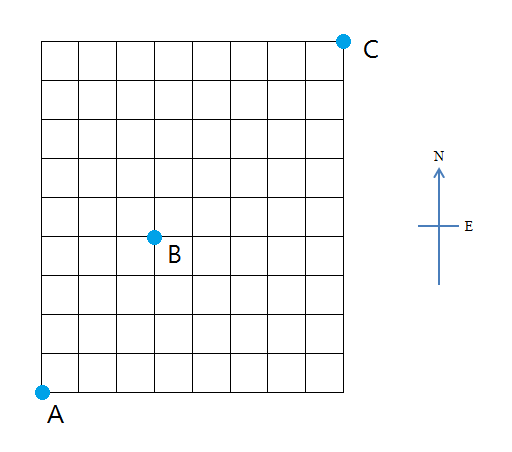
How many ways are there for Ken to complete his journey?

---

Disclaimer: I solved this puzzle in a rush and actually added together the two pieces of the answer rather than multiply them (lol). But regardless, I found the technique to solving this problem riveting and wanted to share my proof.

---

Observation

The number of paths from A to B (denoted (A,B)) is equal to the number of paths from the point one north of A (call it A_0) to B and one east of A (call it A_1) to B.

(A,B) = (A_0,B) + (A_1,B)

This is obvious: A has two choices, north or east, and the total number of paths is equal to the total number of subpaths in each direction.

Let's look at this observation a slightly different way.

Suppose A is N steps west and M steps south of B.

Let's write the path from A to B as (N+M,N): we need to take N+M total steps, and one of the direction is N long. Note that this is equivalent to (N+M,M) because of symmetry: the number of paths going N steps north, M steps east is equivalent to going M steps north and N steps east.

Then we can rewrite our equation above as (N+M,N) = (N+M-1,N) + (N+M-1,N-1)

Claim: The number of paths (N+M,N) is equivalent to N+M choose N.

This is not a large logical leap to make, as the above is a well known formula in combinatorics, but I'll prove it via induction.

Base Cases:
(1,0) = 1 -- there is 1 path upwards
(1,1) = 1 -- there is one path in either direction.
(2,1) = 2 -- you can go right then up, or up then right.
(2,0) = 1 -- you only go one direction til you hit the point.

These all hold for the formulas: 1 choose 0 = 1, 1 choose 1 = 1, 2 choose 1 = 2, 2 choose 0 = 1.

Assume for all numbers 0 <= a,b <= N that (a+b,a) = a+b choose a
By proving this formula for (a+b+1,a), then we can show that one step leads to the next ad infinitum, so the relation holds.

(a+b,a) + (a+b,a-1) = [(a+b) choose a] + [(a+b) choose a-1]

= (a+b)! / (a! * b!) + (a+b)! / [(a-1)! * (b+1)!]

= (a+b)! * [ (b+1) / (a! * (b+1)!) + a / (a! * (b+1)!)]

= (a+b)! * [ (a+b+1) / (a! * (b+1)!)]

= (a+b+1)! / a! * (b+1)!

which is equivalent to (a+b+1) choose a. Thus, by induction, (a+b,a) = (a+b choose a)

So now that we have proven the general case, we can apply this to the example.

B is 7 steps away from A and 3+4 away, so there are (7,3) = 35 paths to it.
C is 10 steps away from B, and 5+5 away, so there are (10,5) = 252 paths to it.

In a rush I mistakenly entered 35+252, but clearly it is 35*252: for each of the 35 ways to get to B, there are 252 ways to get to C.

35*252 = 8820

Fun problem, look forward to competing in the next!

---

My name is Ryan Daut and I'd love to have you as a follower. Click here to go to my page, then click in the upper right corner if you would like to see my blogs and articles regularly.

I am a professional gambler, and my interests include poker, fantasy sports, football, basketball, MMA, health and fitness, rock climbing, mathematics, astrophysics, cryptocurrency, and computer gaming.