Lamentations in a Sanatorium
Sets
Today, I'm going to talk about one of the most monumental result in set theory-- that some infinities are larger than some infinities. This statement is ambiguous of course, in what sense are we comparing infinities exactly? In this post, what we are going to compare are sets, infinite sets, to be exact. But what are sets? To make things simple, we say that a set is just a collection of distinct objects. Sets can be a collection of anything, really, so let's say that S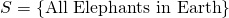 wikipedia page for it. For this post, we'll talk about well-defined sets-- sets in which we know whenever any object is a member of it or not.
wikipedia page for it. For this post, we'll talk about well-defined sets-- sets in which we know whenever any object is a member of it or not.
The Natural numbers and Real numbers
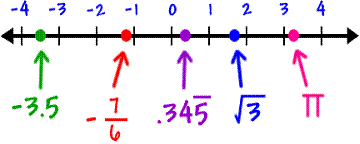
The set of real numbers is comprised of the union of irrational and rational numbers. The rational numbers, which are just the fractions like 1/2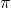 3.14.
3.14.
Comparing Sets
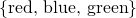
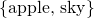 3 elements in it, while the second one only has 2
3 elements in it, while the second one only has 2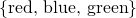
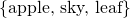 cardinality, since they both have the same number of elements, namely, 3. Seems pretty easy and straightforward right? You just have to count the individual elements of each set after all. Not really, we actually have to refine our technique of comparing sets, it will be apparent later why, but for now let's take a different approach. Let's say we have two sets A and B, and say that A has a cardinality that is greater than or equal to B when for each member or element of B, we can assign to it a distinct member of A
cardinality, since they both have the same number of elements, namely, 3. Seems pretty easy and straightforward right? You just have to count the individual elements of each set after all. Not really, we actually have to refine our technique of comparing sets, it will be apparent later why, but for now let's take a different approach. Let's say we have two sets A and B, and say that A has a cardinality that is greater than or equal to B when for each member or element of B, we can assign to it a distinct member of A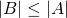
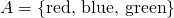
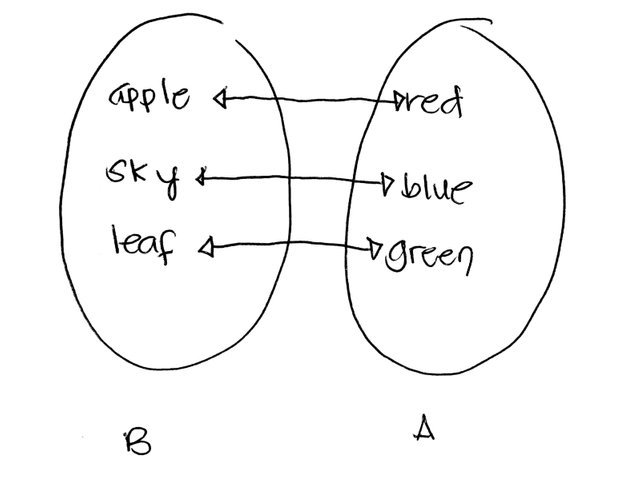
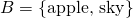 A larger than B, we'll show that this method works just the same: we can assign apple from B to red in A, and sky in B to blue in A as summarized by the illustration below
A larger than B, we'll show that this method works just the same: we can assign apple from B to red in A, and sky in B to blue in A as summarized by the illustration below
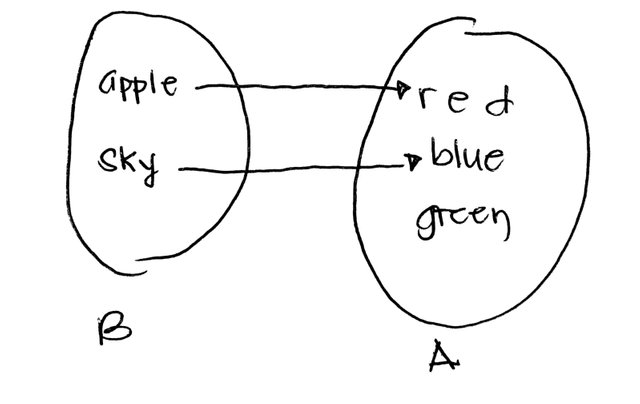
Since we have assigned every member of B to a distinct member of A, then by our definition, A has a larger cardinality than B. Note that it actually doesn't matter how we assign each element above, we can assign apple to green and sky to red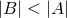
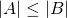 each, I mean ALL) member of A to distinct members of B, one of them will always be left out . From now on, this is how we'll be comparing sets.
each, I mean ALL) member of A to distinct members of B, one of them will always be left out . From now on, this is how we'll be comparing sets.
So what about when A and B have the same cardinality? This is, in a way, easier to understand; A and B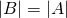
Comparing Infinite Sets

The technique that we used above has the advantage of being able to compare both infinite and finite sets.
The Diagonalization Argument
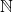
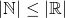 n
n
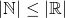 less than or equal the cardinality of the real numbers. This result isn't very satisfying since it tells us something that we already know about, that the naturals are embedded to the reals. Since our last result says "less than or equal
less than or equal the cardinality of the real numbers. This result isn't very satisfying since it tells us something that we already know about, that the naturals are embedded to the reals. Since our last result says "less than or equal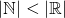
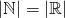
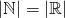
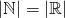 distinct
distinct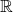 distinct
distinct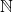 all of the real numbers as if they are like natural numbers like so:
all of the real numbers as if they are like natural numbers like so:
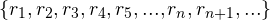
It might get a little confusing from this point on, since book-keeping on both the notations and the digits that will appear might get too cumbersome, but I honestly believe that this is one of the cleverest trick that I have seen in mathematics, so just try to hang on.
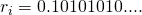 0's and 1's. Since we assumed that all the real numbers can be listed like the one above, we can as well list this subset like natural numbers. So just for demonstration let us give some values to the list of real numbers above:
0's and 1's. Since we assumed that all the real numbers can be listed like the one above, we can as well list this subset like natural numbers. So just for demonstration let us give some values to the list of real numbers above:


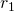 1, we 'flip' it to 0, and this 0
1, we 'flip' it to 0, and this 0

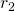 0, so we 'flip' it to 1
0, so we 'flip' it to 1 n'th
n'th n'th
n'th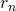

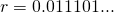
 0
0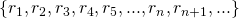
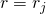 j
j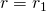

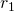
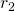 2nd
2nd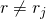 j, because they have different j
j, because they have different j
Quoting Arthur Conan Doyle "Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth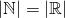
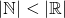
Its Implications
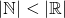 1, we know immediately that 2 is the next whole number, but this is not the case for real numbers. If you start from 1, you do not know what really the 'next' real number is, because they are so 'densely packed' together that there is always another real number between two different real number. To demonstrate, there is always 1/2 between 1 and 2, and between 1 and 1/2, there is 1/4; worse, there's some pi between your 3 and 3.2
1, we know immediately that 2 is the next whole number, but this is not the case for real numbers. If you start from 1, you do not know what really the 'next' real number is, because they are so 'densely packed' together that there is always another real number between two different real number. To demonstrate, there is always 1/2 between 1 and 2, and between 1 and 1/2, there is 1/4; worse, there's some pi between your 3 and 3.2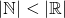
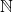
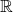
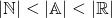 Continuum Hypothesis. Although years later, after refining our foundations of mathematical logic, it was shown to be unprovable-- at least in a sufficiently reasonable set of axioms of set theory, the Continuum Hypothesis turned out to be a statement that can be true and false at the same time. This result came later after the original mathematician who posed the Continuum hypothesis passed away.
Continuum Hypothesis. Although years later, after refining our foundations of mathematical logic, it was shown to be unprovable-- at least in a sufficiently reasonable set of axioms of set theory, the Continuum Hypothesis turned out to be a statement that can be true and false at the same time. This result came later after the original mathematician who posed the Continuum hypothesis passed away.
Georg Cantor
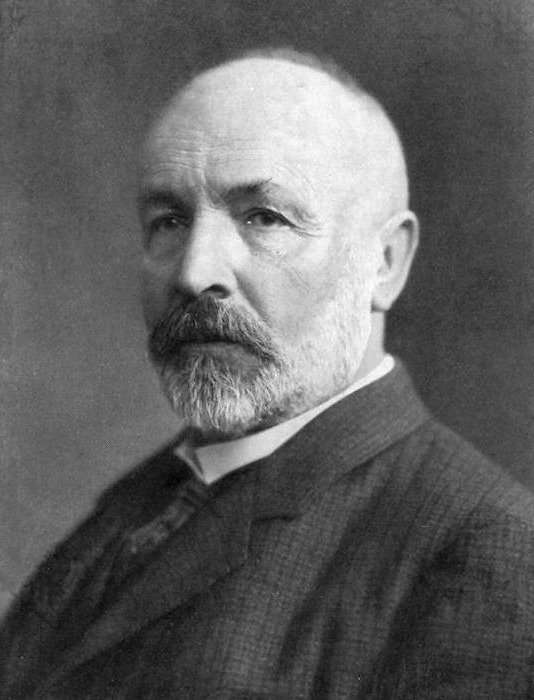
I refrained from referencing him because I wanted to dedicate a whole section to him. All of the results above, we owe to Georg Cantor's genius. He was the one who pioneered the study of Set Theory in its own right, thereby making a huge impact on the foundations of mathematics-- since then mathematical theories were translated into the language of Set Theory. Some mathematicians hailed him, one of them was David Hilbert, who likened his works to paradise, as he made the study of mathematics clearer for everyone. But in his lifetime he was also ostracized by his contemporaries, one of them being his past mentor as his results clashed with his teacher's school of thought. For the remaining years of his life, he was plagued by chronic mental illness including depression-- being criticized by other mathematicians, and not being able to prove the Continuum Hypothesis, which was the brainchild of his Magnum Opus-- the Diagonalization Argument, not knowing that his time still lacks the necessary logical foundation to tackle the problem. He eventually succumbed to a heart attack, dying away from his family in a sanatorium.
Note:
For this post, I just cross checked their respective wikipedia pages, especially on Georg Cantor. For the diagonalization proof, I referenced my old undergrad notes.
This post became longer than I had intended, so it's a lot harder to proofread now. Please let me know if there are any blatant errors above.
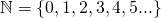
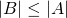
I think that using the examples that you use it makes more sense to talk about countable versus uncountable in this setting. Countable has meaning in a finite and in a single infinite setting while for uncountable there are many different infinite settings.
Also note that by defnition a question cannot be a hypothesis. The continuum hypothesis is there is no set between the cardinality of the natural numbers and the reals.
What do you mean different infinite settings? Do you mean climbing up the 'infinity' ladder by taking power sets of infinite sets? Anyway, I was reluctant on using countables and uncountables because I didn't want to keep introducing new concepts.
Yeah, you're correct about CH, that's embarrassing, I edited the article accordingly. Thank you.
I agree that discussing the general concept of infinity (by which I mean ordinals) is unnecessary for an introduction. I meant to say that if you are only discussing countable and uncountable then you can directly start with this as opposed to starting with infinity which is much broader concept. But this is a matter of taste I think.
Hmm, I guess you're right. It might have been better to center this whole article about countability and uncountability, but obviously, at some point, I got carried away with injections and bijections that I kind of lost the chance to introduce it, I was rushing to get to diagonalization, I really like it lol. This isn't exactly friendly to non-mathematicians I guess.
Congratulations @blackiris! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP