Why is the 0 exponent of a non-zero number equal to 1?
People say that English is a funny language. I bet it is, but how else can you explain that we have noses that run and feet that smell?
Or tell the man that what his car transports is a shipment while if a ship does the same, it is a cargo.
Pretty crazy? I know. But we have not seen the end of the absurd when we take a walk down the mathematical lane.
A zero in English means nought if you are from the UK or thereabouts or naught if you happen to be an American. It means zilch or nothing.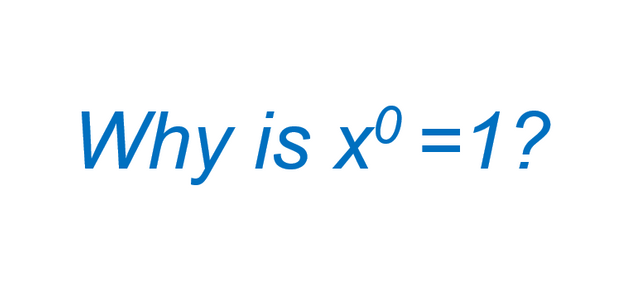
Own Image
But in mathematics, exponentiation, it does something magnificent.
If any number is raised to the power of zero, it automatically becomes 1. That is x0 = 1, with the exception of where x= 0 which may lead to leaving the expression undefined.
This expression is usually taught in the high school mathematics class. We often seem to take it as a law or convention. But nothing in maths is ever that. There is always a proof that something is what it was.
Not all the things we are taught in high school is redundant. I know you may ask what use is knowing that mitochondria are the powerhouse of a cell got to do with paying taxes to the government. That may be the one that may be a little bit redundant, but it may add to make you that awesome doctor that treats the Kim Kardashians and charge $5000 per hour. That is something that would help with the taxes.
Going back to the issue, sometimes we assume that a lot of things in mathematics are just that way. Some of the things we accept as such have proofs which are long lost and buried deep somewhere in a textbook in the dusty shelf of a library.
But when a number is raised to the power of zero, the answer is usually one when the number is not zero. The same is also true on the factorial of zero, i.e. 0! = 1.
Going back to the basics
We will see that the exponential function is a mathematical function which is of the form.
f (a) = xa
i.e xa
Here, x is the constant also known as the base. The a is the variable number which is the power of the function-any number can be here.
In mathematics, we will often run into the exponential-function base known as the transcendental number denoted by e which has the value of 2.71828.
We have in the situation f(x) = ex
When x (exponent) increases by 1, the value of e (the function base) will also follow suit and multiply by 1. The same happens if it decreases or gets divided.
In the beginning, we can only raise a constant by positive numbers. With time there was an expansion of the function's domain such that we can about raise a constant to any number starting off from a fraction, complex number, negative number including negative fraction, etc.
The exponential function is a mathematical representation of the number of times a number will have to undergo self-multiplication.
For example, 23 represents that the base function 2 undergo multiplication three times, i.e. 2x2x2 which of course is 8.
23= 8
But when you try 64 1/3 we get an answer that is the outcome of the cube root of 64 which is 4.
i.e. 3√64 = 4
This conjecture invariably shows that the when a number is raised to a fractional exponent, that it expresses the root of the base number.
More example, a 5121/3 = 3√512= 8
8x8x8= 512
But when an exponent is a negative number, the base number will have one divide it, and the negative exponent becomes positive.
For instance, 2-3 can be expressed as (1/2)3
Let's prove that x0 = 1 Assuming we have two variables xa and xb. If we divide the first variable by the second, xa/xb = xa+(-b) xa+(-b) = xa-b If a=b, then the right side of the equation gives x0. But xa/xb = xa+(-b)= x0 And we have a=b Then the left side of the equation is given as xa/xb = xa/xa = 1 x0 = 1 We have the proof REFERENCES


I've once been shown this in my further maths class, but I obviously didn't pay attention...haha.
You are not alone. I never pay attention much in class. Guess you could say it's something to do with how uncomfortable classes can be.
Absolutely! Although I loved ordinary maths in my high school days and could afford to defer the uncomfortable conditions for it, strangely, my further maths classes do not have same history.
That's great to hear. Looks like you've made peace with maths now :)
I had never had the time to ascertain why this was so. I simply apply the methods. good to see how it came about, sir.
You guys, the engagement officers, are doing a wonderful job. Kudos
Any nonzero number raised to the zero power is equal to one (i.e., n0=1). This concludes that all nonzero numbers raised to the zero power are equivalent because they all equal 1. learned something. Thanks for this.
The basic algebra rule that makes it easy to get work done. Thank you.
You should be called simplicity King. I so much love the way you broke it down..This is definitely simple to follow
I have always known this but never bothered about knowing how it's proved. I guess that's why we have @steemstem and the best tutor @bitfairy
I am blushing right here. But you wouldn't know as I'm as dark as night. Lol. Thank you for that great compliment.
Lol. Dark but illuminatintg...Well-done
:)
I never really stop to check how many maths function is derived. I just use it. I know its weird, but that is just how I flow.
I do that too. It is just like riding a bicycle, once you know how you do it any way. Thank you.
It becomes so much easier when applying a principle that you know it's origin. Although sometimes it's best not to ask questions about some. I guess that's just the nature of maths.
Well done @bitfairy.
We can always take out time to check some of them. Thank you.
Great explanation and very easy to follow!
I remember one day our Math teacher trick us by doing all sort of weird calculations in which he "demonstrated" that 2+2 could be = 5.
I know he must have made some quick trick but we weren't able to catch it, I will always remember that because every calculation he did made completely sense, and the final result was that indeed 2+2 = 5...
I wish I could remember how he did it, but that must have been a trick for sure.
I like such teachers that make learning fun. Most people thought maths was tough due to the teacher that taught them the basics. If it's a lively teacher that does all those tricks in classes, learning can then be fun.
No. Ιt's multiplication, we sum exponents in this case.
x^a * x^b=x^(a+b), and therefore if a=b, then x^a * x^b= x^2a (or x^2b)
This example you used works in case we divide those variables x^a and x^b (or you probably forgot the minus sign on the b exponent).
Regardless, upvoted. Good job!
You are right, it is division. Thank you for pointing it out.
Noted. thanks for pointing that out.