Transformation Geometry
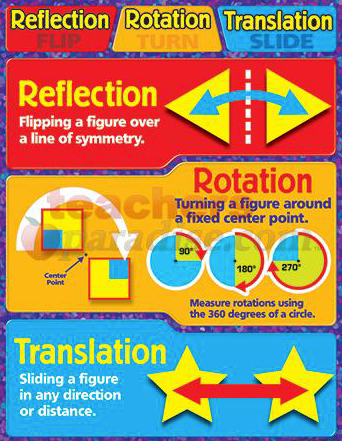
We get 3 different types of transformations
To transform shapes, means to change them. Transforming 2D shapes, is the change made to the specific shape.
We can transform a shape by moving it (translation), reflecting the shape (reflection) or by rotating the shape (rotation)
In this lesson we are going to look at rigid transformations. This means that the the size and the shape used, will remain unchanged. The original shape is called the object, and the the transformation of the shape is called the image.
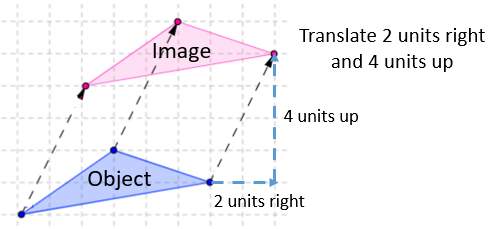
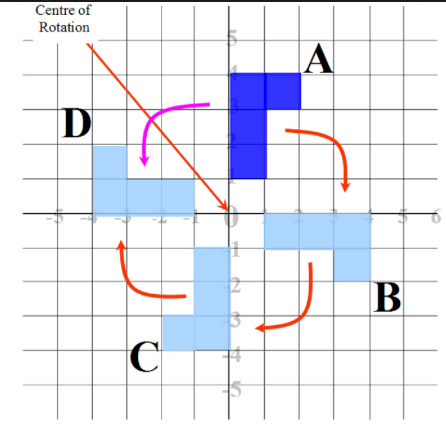
Note that the object is translated 2 units to the right and 4 units up and NOT the image translated 4 units down and 2 units to the left.
1. Translation
Translation means to move an object without changing the size or the shape. A shape can be moved by a fixed distance, up, down, left or right.
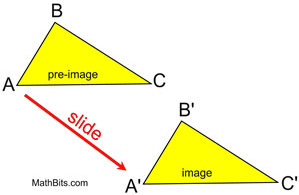
Moving an object or a translation of an object can also be referred to as a slide. You slide the object to get the image.
When we we write the answer of translation, we don't always have to state where the object or the image will be. For the above example, triangle ABC is translated to triangle A'B'C'. ABC is the object and A'B'C' is the image.
It is always essential to state the direction of the translation as well as the distance if possible. In gr 7, we learn about translation, just that the shapes are moving in a direction. Use grid paper to draw the shapes and then learners can also see what the distance will be and in which direction the object is translated.
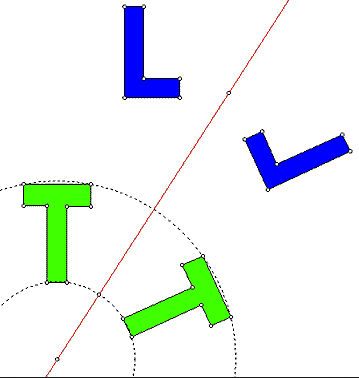
2. Rotation
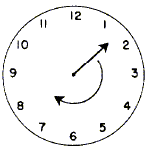
The 2nd transformation that we are going to look at, is rotation. A 2D shape is turned around a point. This point is called the point of rotation.
We can describe the rotation as a clockwise or anti clockwise rotation.
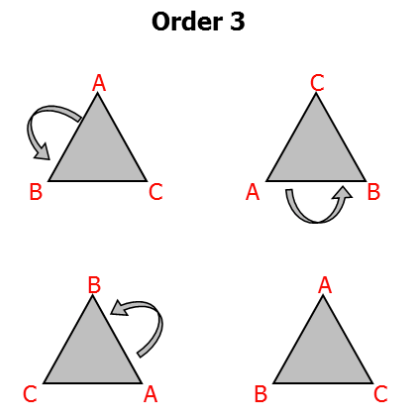
The number of positions a shape can be rotated to, without making any changes to what the shape look like is called the order of rotational symmetry. (How many times can a shape rotate, to get back into its original position)
An equilateral triangle has an order of rotational symmetry of 3.
Order of rotational symmetry is 3
The equilateral triangle is rotated 3 times to get back into its original position.
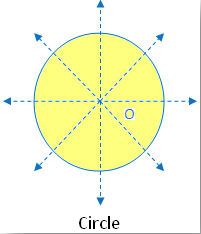
A circle can rotate through any angle and will always look the same. A circle has an infinite order of rotational symmetry.
The shapes above has been rotated around the same point
3. Reflection
The 3rd and last transformation is called reflection. Think of looking at yourself in a mirror, you see a reflection of yourself. This works the same with shapes, they are a reflection of each other. Reflection flips over a mirror line called the line of symmetry. The line of symmetry divides shapes or figures into two mirror-image halves.A shape can be reflected up, down, left or right.
A reflection image of a butterfly, one half of the butterfly is the same as the other half
The red line in the middle of the letters is the line of symmetry.