Geometry of 3D shapes - Lesson 2a - Prisms
Prisms
In geometry, a prism is a polyhedron comprising an n-sided polygonal base , a second base which is a translated copy (rigidly moved without rotation) of the first, and n other faces (necessarily all parallelograms) joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named for their bases, so a prism with a pentagonal base is called a pentagonal prism. The prisms are a subclass of the prismatoids.
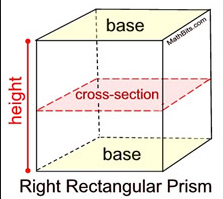
A rectangular prism with 2 base ends and a cross section
A prism is a 3D that has a constant cross section. It has a pair of parallel faces, that are also congruent polygons. The cross section of the shape stays the same and are called the ends of the prism or the base end.
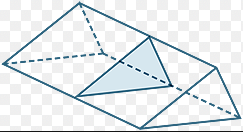
A triangular prism with a cross section
If you cut a prism along the length from one end to the other, it will have the same cross section along the whole length. The cut you make, must be parallel to the ends of the prism.
Regular and irregular prisms
If the end shape of the prism is a regular polygon, then we call the prism a regular prism. If the end shape is not a regular polygon, we call in an irregular prism.
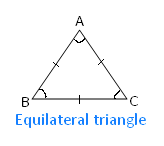
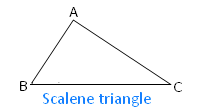
A regular polygon has sides of equal length and an irregular polygon has sides of different length.
Regular polygon:
A polygon which has all its sides of equal length and all its angles of equal measures is called a regular polygon.
An equilateral triangle is an example of a regular polygon.
Irregular polygon:A polygon which has all its sides of unequal length and all its angles of unequal measures is called an irregular polygon.
A scalene triangle is an example of an irregular polygon
Other names for polygons:
We also name shapes with:
- 5 sides - pentagon
- 6 sides - hexagon
- 7 sides - heptagon
- 8 sides - octagon
- 9 sides - nonagon
- 10 sides - decagon
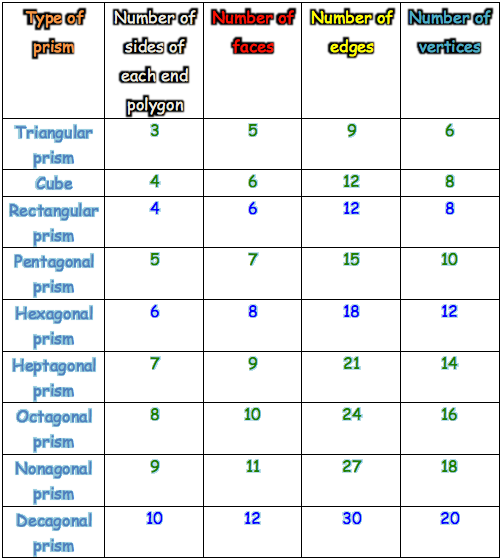
Properties of prisms:
In the following table we can see the properties of 3D shapes that grade 7 learners must know:
If we have the end polygon, it will be easy to calculate the number of faces, vertices and edges of each 3D prism.
To calculate the number of faces, we can say that it is the end polygon + 2
To calculate the number of edges, we can say it is the end polygon x 3
To calculate the number of vertices, we can say that it is the end polygon x 2
In all 3 of the above, we use the end polygon to calculate each of the faces, edges and vertices.