Lottery mathematics - to play or not to play, that is the question...
I always considered probability to be a long-lost love child that mother math had with father crystal ball forecasting of the future. Women have always been attracted to bad boys, do not judge her. Probability grew up to be both appealing and mysterious as her father and yet intelligent and strict like her mother. Visitation rights? Probability lives with her mom and talking about the good old dad is considered to be a taboo topic so visiting him is out of the question. Like most regreting moms, math gets angry when the kid mentions her father. You could say that probability is not living in a healthy environment but hey, aren't girls with "daddy issues" fun to be around and play with? It is almost Shakespearean, to play or not to play?

CC0 licence, Pixabay, author: geralt, adapted by me
Some years ago when I was in college and attending a class called "Statistics and probability", the professor was very open about his opinion on how the lottery is tax on fools. Who knows, maybe he has daddy issues too but that is beside the point. The point is not to have a mathematical debate about this but a philosophical one too. Hmmm... Since we can not have a mathematical debate, let's say that we will have a philosophical debate about mathematical results. Yes, such a thing is possible. Mathematicians do not usually like it, but it is possible. Remember my question from the title, I am curious what your answer will be by the end of this post and if you answer it now, will your opinion change or remain the same. Ready, set, go math time! Mmm, with some philosophy too, of course...


Before we get into calculating your probability to win those millions, we first need to introduce you to some simple terms that will help you figure out the more complicated stuff later on. We will go over 3 things, probability of an event, combination, and permutation.
Probability first
Some event can happen with a probability 0, 1, or anything in between where 0 means that it will NOT happen, it is impossible, and 1 that it WILL happen for certain. For example, we may say that I have the probability of 0 to grow a third arm coming out of my forehead and I have the probability of 1 to have a pen in my hand if I pick up a pen from the table. Probability can be expressed with decimal numbers, fractions, or percentages so 0.5, 1/2, and 50% mean the same. How do we calculate probability? By dividing the number of ways an event can happen with the total number of outcomes.
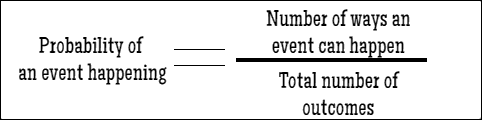
Image 1. probability equation, author: @zen-art
We can easily see how this works by looking at the example with balls in a container. Imagine a situation where you have a container with some balls in it. There are 4 green balls, 2 blue ones, and one red ball in there. All balls are equal in their shape, size, weight and are same on the touch. Without looking, you reach your hand in there and take one ball out. What are the chances that the ball will be green? What are the chances the ball will be anything but green? What are the chances of the ball being red?
Since there are seven balls in there, the total number of outcomes is seven. You can take one of the seven balls so there are seven possible scenarios or outcomes. As for the number of ways a specific event can happen, it depends on what we are looking for. If we are interested in the possibility of the ball to be green than that number is 4 because there are 4 situations possible for that ball to be green. If we are looking for the possibility of the ball being blue or red, there are 3 ways that could happen because there are 3 balls that we can pick up and find them not green. There is only one scenario where the ball picked up is red.
This seems pretty easy, right? That's because it is. Dividing two numbers is not that complicated to do, once you have those two numbers. The tricky thing is coming up with the correct and precise numbers for the way an event can happen and the total number of outcomes possible. This is where combinations and permutations come to join in the party.
Permuation
Have you ever watched a spy movie and get annoyed when someone says the combination of the safe is...? I have. If the numbers that unlock that safe are 1452, that is not its combination, it is its permutation. You do not have a pin combination, you have a pin permutation.
When the order does not matter then we can say something is a combination but when the order of things matters, it is a permutation. For example, some meadow is a combination of violets, daisies, and clovers but the pin number for someone's credit card is 1234. 4132 or any other permutation will not work.
We can have permutation with or without repetition. With those pin numbers, repetition is allowed and the pin can just as easily be 1111 as it can be 1234 but there are things where repetition is not allowed.
For permutations with repetitions, let's say the pin number with 4 digits, the first digit can be 10 different numbers, the second one can be 10 different numbers and so on and we have n*n*n*... (r times) or n^r. In this case: 10*10*10*10 or 10^4. That means there are 10 000 different pin numbers you can make with digits 1 to 9, and 0.
What about permutations
without repetitions?
Imagine that you have to choose 3 lectures to attend during your weekend out of 10 that are going on around your city. Without repetition, your choices get smaller each time. You have 10 to choose from for your first lecture, 9 for the second one and 8 for the third because you can not choose what you have already chosen. That means you have 10*9*8=720. This is where factorial function comes in handy.
Factorial function tells you to multiply all the numbers coming up to yours and we denote it with !. For example, 3!=1*2*3=6 or 7!=1*2*3*4*5*6*7=5040. Why do we need this here? We can mathematically write that which we have talked about a moment ago. That comes in handy because not all math problems are that simple and easily solved. To get the number of permutations for your 3 lectures out of 10 we will use the following formula:

Image 3. Permutation, author: @zen-art
In our example with lectures that would be P(10,3)=10!/(10-3)!=10!/7!=(10*9*8*7*6*5*4*3*2*1)/(7*6*5*4*3*2*1) or (10*9*8*7!)/7!=10*9*8=720 That means that there are 720 permutations for you to choose your 3 lectures out of 10. Lottery, on the other hand, goes beyond this. Lottery is all about combinations, not permutations. So... Why did I bother you with this? I did not say you will not need it...
Combination
In combination, order does not matter. Like permutation, a combination can also be with or without repetition. Combination without repetition is how the lottery works. It is only important what numbers are drawn, not in what order and there are no repetitions. We start by using permutation formula and we reduce it to eliminate the repeating combinations.
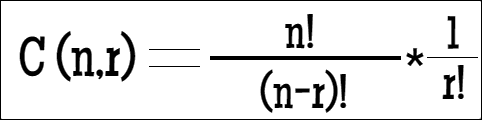
Image 4. Combination, author: @zen-art
The only thing that we did there is we removed what we did not want. For example, if we wanted combinations for 4 out of 10 numbers, 1234 is fine to be among combinations but 2134,4321 and so on we do not need. Best way to remove permutations is division. We want to remove extra permutations and we do that by dividing permutation count by r! That is why r! needs to be in the denominator. The equation above is often presented in its shorter form called binominal coefficient.

Image 5. Combination, binominal coefficient author: @zen-art

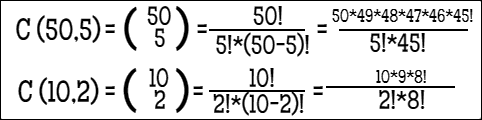
Image 5. Lottery calculation first part, author: @zen-art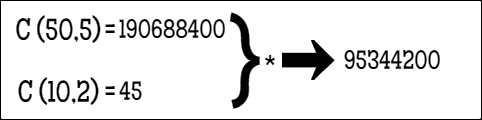
Image 6. Lottery calculation second part, author: @zen-artAnd your probability
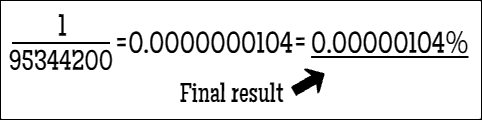
Image 5. Lottery calculation, final part, author: @zen-art


Image 5. Combination, binominal coefficient author: @zen-art


Every Friday, EuroJackpot lottery is taking part and people from most of the countries in Europe can participate by buying a ticket. Since there are many players, possible winnings are huge. The main jackpot expected in two days is around 18 million euros or 20 million dollars.
To win the biggest prize, you have to pick the correct 5 out of 50 numbers and 2 out of 10, both those combinations have to be correct because even though your correct 5 out of 50 numbers will win you a lot, you will win more if you guess those two additional ones. We have two events happening at the same time; event 5 out of 50 and the event 2 out of 10. Probabilities here are multiplied. When you want to find the probability for two events or "AND" events, you multiply and when you want to find "OR" you add. For example, if you want to find the probability of one dice landing on 5 or 3, you would add but for a dice landing on 5 and a coin landing on tales, you would multiply the possibilities. This is why we can calculate the combinations for 5 out of 50 and 2 out of 10 and then multiply them to get the total number of combinations.
Ready?
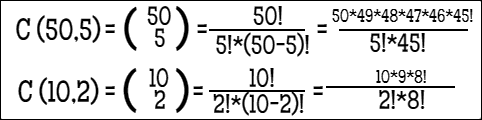
Image 5. Lottery calculation first part, author: @zen-art
I have done these two calculations simultaneously and after some fraction abbreviates to simplify the things I will enter into my calculator, I got this:
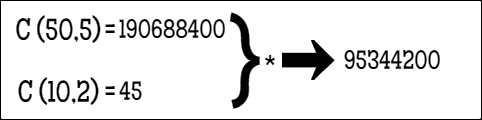
Image 6. Lottery calculation second part, author: @zen-art
As you can see, the number I got is 95344200. What is that number exactly? It is the number of possible combinations to pick 5 out of 50 and 2 out of 10 numbers. This is still not the probability to win the EuroJackpot. Remember that main definition for the probability that I told you about at the beginning? It says that the probability of an event happening is equal to the number of ways an event can happen divided by the total number of outcomes. The number that I just calculated is the total number of outcomes. What is the number of ways the event can happen? ONE. There is only one correct combination of numbers that will be drawn. The final step is dividing 1 by 95344200.
And your probability
of winning the EuroJackpot is:
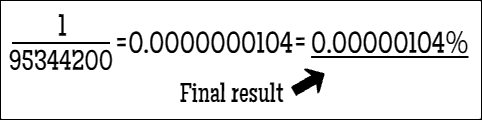
Image 5. Lottery calculation, final part, author: @zen-art


The math is solid. Your probability of winning the EuroJackpot is 0.00000104% or 1/95344200 if you prefer the fractions. Should you play? Most of the mathematicians will advise you not to do it (luckily for you, I am not a mathematician) and save your money instead. Maybe they will even call you a fool like my professor did but let me tell you something very important. It is not a secret really, just a change of perspective. People have won the lottery. They had the same probability of winning like you have. The only two probabilities that matter are 0% and 100%. Everything in between means nothing to you. Probability does not predict anything. It gives you the chances of things happening but it does not predict what will happen. As long as the probability for you winning is not zero, you have a chance.
To play or not to play?
You could play your entire life and not win. You could play only once and win. You could choose any numbers, even 1,2,3,4,5, because every combination has the same probability. You could waste your time and google the secrets behind choosing the right numbers (there is no secret of right numbers) or read how you have better chances of being struck by a lighting 3 times than to win the lottery. I hope you do not get struck by a lightning and if you do win the lottery, remember me and this post, maybe throw some money my way :D. So tell me, based on the probability that I have given you... To play or not to play? Want to know my opinion about this? PLAY is the important word here. That is my opinion. If my inner child wants to have some fun, who am I to stop her?
References for this post:
Honestly, I learned all this in college and I can not be certain about the book I was using back then, I think it was one of these two:
- Serdar, Vladimir, Udžbenik statistike, Školska knjiga, Zagreb, 1977
- Sarapa, Nikola, Vjerojatnost i statistika; 1. dio, Školska knjiga, Zagreb, 1993
To check if my memory served me right (and it did), this page helped:
Probability of events from mathplanet.com
Until next time,


- all images used in this post are free for commercial use, they are royalty free with the links to original images provided under them



@steemitbloggers
Until next time,
KEEP YOUR SMILE ON,
AND HAVE FUN!

P.S. All that intro about probability being the long lost love child between math and crystal ball forecasting of the future... If you somehow got offended by that, sorry. My inner child made me do it...😎

Image sources AND LICENCES in order of appearance:
- all images used in this post are free for commercial use, they are royalty free with the links to original images provided under them
- line divider that I use is from FREE CLIPART LIBRARY, and is here
- titles are made by me using a royality free photo from pixabay that can be found here
- my bitmoji avatar was created on https://www.bitmoji.com/, visit the site to create yourown
PROUD MEMBER OF:



@steemitbloggers




i'll play but your math not understand.....sorry dont mind. 👩❤

hahahahaha, I do not mind :D
thanks my friend zen-art
Phew! I was so happy when you got to the familiar territory of mathematics! I was completely lost with the mother and father analogy...
Really? That was some of my best work lol :D
I am glad you enjoyed the post 💚
Ha ha! I'm sure there are people who are the other way around and preferred the poetic imagery of the mother and father instead of the mathematics!
I will never play the lottery. Partially because the odds of winning are stacked against, and partially because I used to have a job selling lottery tickets at a gas station.
We would have these people who spend HOURS doing the following: walk in, buy a twenty dollar scratch ticket, walk out to their car, scratch it, come in to either redeem a paltry amount or throw it away, and then buy another one. Again and again.
Thus, I have a very negative predisposition towards anything lottery related.
That must have been funny to look at. Poor people, they have taken all the fun out of it :)
The format of your posts is amazing.
I once asked my brother why he would spend money (not much, just a ticket a week). He just replies I am aware it is against the odds but still the illusion and thrill last for the week, and that is cheap lol
Your brother is a wise man, wise man indeed. He gets the point :) Thank you for your lovely comment honey 💚
He is very funny and very positive about almost everything :), always laughing and with a smile in his face... he's kind of happy go lucky :) in that aspect!
This is one of my favorite posts that you've written yet! Probability is fascinating to me. And I learned something new! I never knew that combination didn't imply order and that had to be permutation. Thank you!
I am really glad that you enjoyed it and thankful for your feedback. 💚
When do you find the time to write such brilliant posts with an amazing formatting?
Time is just an illusion and I live in multiple dimensions at once ;)
the way you make complex things appear so easy to understand is wonderful
That is very nice of you to say, thank you so much 💚
Most welcome 👍😎
Math solves a lot of things, maybe everything. Lottery is something else. I never buy any lottery tickets. The thought of how much money being spent on a regular basis... chances are you are putting out more money than you would be winning it.
A lot of money is being spent yes but I can not imagine spending 20 million dollars so if I ever win in my life, my winnings will be bigger than what I have spent on tickets :) Some people buy a beer a day, I buy a ticket a week ;)
Wow what a post, it must've taken you hours to put this together. 👍
I rarely buy a ticket, usually only as a group buy at work.
This one did take me hours because there was always something interrupting me yesterday :D I am glad you enjoyed it 💚
I'm going to be very honest because numbers scare me, I searched for your conclusion after seeing the numbers but admiring the pretty formatting you did on your post (I am visual after all :D) - and I found this:
Well, that's a 100% how I see the world and I applaud you :D
hahahahaha :D They do not have scary teeth and they will not hurt you. I promise you, my posts are written in a way that anyone could follow along. Go back when you catch some time and read the post without scrolling. Thank you for your honesty and your support 💚
They did hurt me, a lot, when I was a teenager they attacked me and I just couldn't understand them and want to have anything to do with them. Both maths and economics gave me bad grades which was also displayed in numbers (like a 4,7 on a 10-scale). Then I got to University and someone explained me in statistics class why I needed some of those numbers, and I was like 'aaaahhh - well NOW it makes sense'. It still baffles me I needed to go to University to understand what I had been doing in secondary school. Statistics were still hard, but at least I had found some motivation and 'hooks' to try and understand them.
Anyway, the post indeed deserved to be read, so I went back and did it. I could follow it all :D So that's a huge plus. In Dutch we don't use the combination word (we just use 'code' for something that needs numbers in order to open it) but I still learned from that, I hadn't even heard of the word permutation before, ever.
See? I read a post about numbers and what I'm focussing on is the language and meaning of words.
Runs off to Google pretty images now, enough numbers seen for at least a week!
See, I told you so! :)