Stem-Chess: An Universe of Mathematics Present in Chess
Regards esteemed members of #stem-espanol and community of Steemit in general! This article is following the theme of the discussion of last month, organized by me, @ydavgonzalez, next to @eniolw, @eliaschess333, and @vjap55 in the general chat of the Discord channel of #stem-espanol.
The subject of the discussion was the promotion and socialization of knowledge around chess. Focused on analyzing it from the multidisciplinary approach of STEM, bringing evidence to attract your interest, research and scientific application, this is the way I see the relationship between sport and science, chess and mathematics.
Chess is a sport in which the scientific method can be applied to analyze the nature of the game. From this perspective, as a science of models and abstractions, mathematics is the science to have the highest relevance with it. Many of the situations presented on the chessboard can be represented by formal structures that, although they were created for other purposes, have applications in the chess field.
In the present article, a series of mathematical aspects that take part on the 64 squares of the chessboard will be approached. To start with, I will present a very famous legend about the origin of the so-called “science game.”

Chessboard. Source: PIRO4D(2017) CC0. Pixabay.
The legend of the rice grains
One thousand five hundred years ago, Kaid, a mighty king of India, after having achieved everything he wanted in life, ended up in a chronic state of boredom and sadness. He asked the sage Sissa Ben Dahir to help him, and the later invented a game for the king—chess. King Kaid learned quickly, became enthusiastic and came out of his lethargy, and one day asked Sissa, “How can I reward you?” “Your Majesty,” replied the sage, “all I ask is that you accomplish this: place one grain of rice in the first square of the board, two grains in the second square, four grains in the third square and so on and so forth, bending the grains of rice successively until filling the 64 squares.” Although it seemed a reasonable task, King Kaid could never live up to it.
In image N° 1, we get an idea of how many grains of rice the king should have given to the wise man.

Image N° 1: Grains of rice for each square of the board according to the promise of King Kaid to the wise Sissa. Source: @ydavgonzalez
That is, for the last square of the board the king was to give the wise:
The total of rice grains is calculated by adding:
In other words, the sum of terms of a geometric progression of the form:
The sum of the terms of this type of geometric progression is equal to:
That for the case of the legend of rice grains:
That is, 18 trillion grains of rice which is equivalent to more than two thousand years of the global harvest of this cereal. Therefore, the king could not fulfill his promise.
The horse problem
Various chess problems have attracted the attention of mathematicians since antiquity. One of the best-known examples of this type of situation is the so-called horse problem. Given a chess board, and taking into account the movement of the horse (in the form of L), we must find a sequence of moves by which a horse starting in one of the squares of the board crosses all the boxes passing through each one only once.
There are two types of solutions—closed road, in which the horse returns to its initial square and an open way, in which it does not return. In image N° 2, we can see a typical solution to the horse problem (closed road) where number 1 indicates the initial position of the horse and the numbers that follow 2, 3, 4, etc.—the following movements.
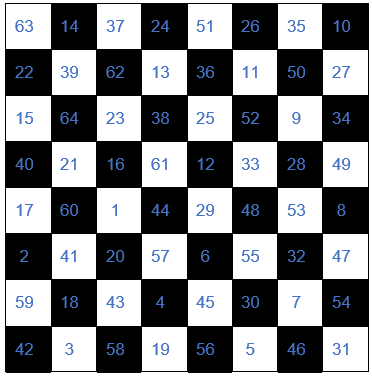
Image N° 2: A typical solution to the horse problem (closed road) Source: @ydavgonzalez
This problem known since ancient times is circumscribed within the branch of mathematics known as the graph theory. Specifically, the problem of the horse would be a variant of the so-called problem of the Hamiltonian cycle which focuses on finding a Hamiltonian path within a given graph.
This problem has been addressed by several mathematicians, including Leonhard Euler, and several studies have been carried out on variants of the problem, such as making the route on a 10×10 board.
Value Material of the pieces
Any chess player understands the importance of the material in the development of the game (number and type of pieces of each player). An advantage of only one or two pawns is often decisive for the outcome of the game, and little can be done when the adversary owns a bishop or a horse more than we do but we have some compensation for it.
However, in various situations, there are quite heterogeneous material relationships. For example, one side can be faced with two rooks and three pawns to a queen and two pawns in which case it is useful to have a way of valuing these positions.
To analyze this type of situation, a series of material evaluations have been created that allow quantifying the value of the pieces that each player has on the board. Although it is true that different authors indicate different ratings for each piece, most agree on using the pawn as a calculation unit. In this way, the value of the other pieces is constructed from this base.
A standard assessment is as follows:
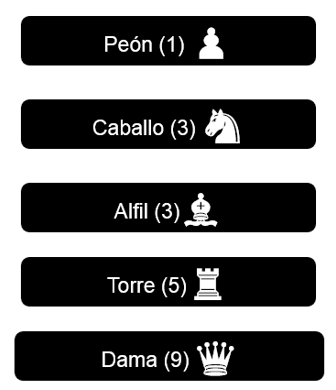
Image N° 3: Example of material evaluation of chess pieces. Source: @ydavgonzalez
From this assessment can be established that a rook has a value higher than a horse or a bishop (an advantage that is often called “quality”) and that the queen, due to its exceptional ability to move, has a value much higher than the other pieces.
On the one hand, the games of amateur players are usually decided by some material advantage obtained by virtue of the errors of the opponent. However, in high-level games, it is generally tough to gain a material advantage, which is why other players intervene. From a theoretical consideration about a position, it is the accumulation of small advantages that tilts the balance towards one of the sides.
On the other hand, although there is a series of material values for each piece, the position also influences the real value of each piece. In this sense, we can speak of a dynamic value which depends on the position and modifies the valuation at the moment to perform the analysis.
Can a game of chess be infinite?
One of the big questions about chess is whether a game can be infinite, that is if there can be a sequence of solid plays so that the game never ends (assuming there is no time control that limits the duration of the game). Concerning this question FIDE (The Fédération Internationale des Échecs or World Chess Federation) has established two rules that limit the length of the game in a number of moves:
- A game is a draw if the player correctly claims when a position repeats at least the three times.
- A game is a draw when after 50 moves, completed by both the white and the black, no pawn has been moved and no piece has been captured.
Based on these two rules, a maximum limit is established for the duration of a game. Therefore, chess games have a finite number of moves.
Mathematical curiosities in chess
There are several curious facts with which mathematics shows us the great complexity of chess. One of those is the so-called Shannon number which is an estimate of the complexity of the chess tree, that is, the number of possible games.
Claude Shannon estimated this number taking into account that in each movement each player has an average of 30 options and as in each game an average of 40 is played, the Shannon number is approximately equal to:
At present, closer approximations place the value of Shannon’s number at 10123, To get an idea of how significant this number is, we must bear in mind that the number of atoms in the universe is estimated at 1080,An impressive fact is that in the universe there are more possible chess games than atoms.
Chess and game theory
The branch of mathematics that is responsible for studying games is known as game theory. This discipline is applied to model the games and represent them as mathematical structures, and also has a series of applications in various areas of human activity and economics.
Within game theory, chess is classified as a non-cooperative game because each player bases the choices on the personal benefit; it is also a zero-sum game, that is, a player’s gain is balanced by the adversary’s losses. For example, when a player obtains a piece of advantage, the obtained material value also represents the disadvantage that the opponent has at that moment.
At the moment of making decisions, the players base those on the Minimax Criterion (each player must minimize their maximum loss). Because this is truly applied to each play, it confirms the almost absolute absence of chance in the game of chess.
Some geometric aspects of chess
Chess is played on a board of 64 squares (8 rows by 8 columns) whit alternating colors between black and white (in some boards the combination of colors may vary). The pieces follow specific rules of movement, i. e., the towers move in straight lines, the bishops— in diagonals of the same color, etc.
All these particularities give chess geometric properties which are reflected on the board. In the Cartesian plane, for example, the shortest distance between two points is a straight line, and while in chess the movement of some pieces does not follow this rule, a clear example is that of the king (image N ° 4)
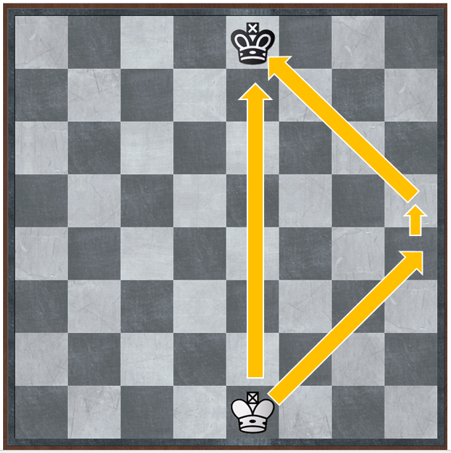
Image N° 4: Tour of the king from the first to the eighth row. Source: @ydavgonzalez
Image N° 4 shows how the king can go following a straight line from square e1 to square e8 in only 7 movements. However, it can also alternate the route along the path indicated by the arrows to the right, and in this case, it also takes 7 movements. This fact shows that the shortest path is not just the straight line that joins the two points.
Another important aspect about the geometry of chess is the rule of the square which states that in a final of a king and a pawn, if the pawn is close to its coronation and the allied king cannot support it, the pawn manages to crown if the opposing king cannot enter the square formed by the squares that the pawn is missing to be crowned, or otherwise cannot extend a square with an equal number of squares in the direction of the adversary king (image N ° 5).

Imagen N° 5 Image N° 5: Rule of the Square; the black pawn is missing only three (3) movements to crown. Source: @ydavgonzalez
In image N° 5, if the white king manages to enter the square, the pawn will be captured at some point along its route.

Image N° 6: Center of the chessboard. Source: @ydavgonzalez
Another aspect of the geometry of a chessboard is the existence of a center. As seen in picture N° 6, the four (4) squares inside the red square represent the center, and its importance is not only in it being the geometric center of the board, but it also gives a substantial positional advantage to the side that controls this domain throughout the entire game.
Mathematical foundations of the International Classification System used in chess
The FIDE organization that rules international chess has created an International Ranking classification system known as ELO Ranking, in honor of its creator Arpad Elo (1903 – 1992). In this system, each player possesses a score depending on the strength of play. The ELO Ranking has a mathematical foundation directly related to the logistic function and in this sense, if player 1 has an ELO score of Pa and player 2— an ELO score of Pb, then, player 1 has a probability in his favor of
while player 2 has
For example, if player 1 has ELO of 2000 points and player 2 of 1600, player 1 has a probability in his favor of
That makes a probability of 90.91% in favor of player 1, which is the mathematical basis of the system used by FIDE to classify all chess players of the different national federations of the world.
Bibliographic References and Material Consulted
González R. (2015), Matemáticas y Ajedrez, Universidad de Murcia trabajo de fin de grado.
Larousse del Ajedrez (2003). SPES Editorial.
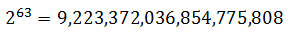
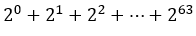
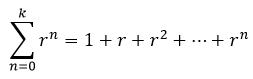
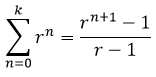
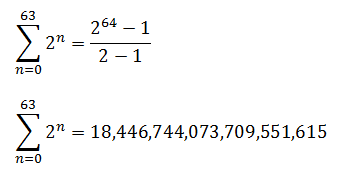
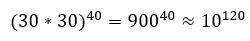
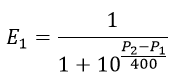
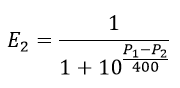
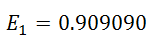
Hola, gracias por apoyarme pero te diré algo. eso de las matemáticas y el ajedrez pues no va conmigo, disculpa mi franqueza pero es que yo no entiendo nada de esas cosas y a veces me siento un poco frustrada por eso. Lo mio es el arte. Así que disculpa nuevamente por mi ignorancia. De todas maneras le voy a dar tu mensaje a un amigo mio que sí sabe de ajedrez.
Gracias por el apoyo, saludos @neyda1975.