If a polynomial has real coefficients, then why do its zeros come in complex conjugate pairs?
If 
and 
are Real Number coefficients, then why do the zeros come in complex conjugate pairs.
For example, if (a + bi) is zero then why is (a - bi) also zero?
I really like this problem, and I hope your answer/proof is correct.
You can see this in your picture. Complex numers with i part +- are mirrored. They can be transformed to r and phi notation building a circle. Knowing that isnt there 2 more complex numbers that can result into 0 as you described? E.g. (a + bi) = 0, then should aslo (-a + bi) and (-a - bi). These would be lying in the other half of the circle.
If a math genius reads this and im wrong please correct me or explain better ;-)
J
That may be a way to answer it, but a proof requires completion. I actually think geometric proofs are the best of any kind of logic because they are the purest. The way I solve this uses algebra though. It's actually just a direct result of the additive and multiplicative properties of complex numbers. So if we know that a complex solution to the polynomial (when you plug this in the polynomial you get zero) is as follows:
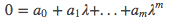
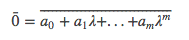
then the complex conjugate is this:
which is clearly zero (because the complex conjugate of a real number is the very same real number).
If you could find a geometric proof for this though I would be very interested.
A really cool way to answer this in one sentence that I just thought of goes like this:
If there exists a complex solution to the polynomial, then the complex conjugate is also a solution because the complex conjugate of zero is also zero.