Math Art: Proving the Yin Yang has an Equal Area of Black and White
The Construction

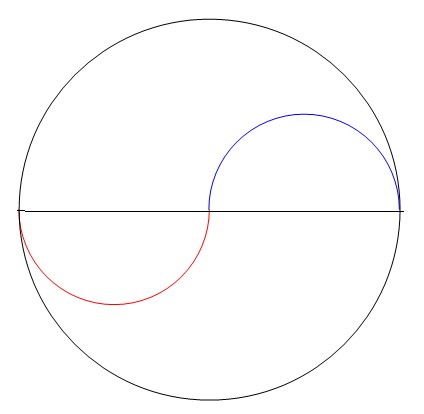
In order to figure out the area of the Yin Yang I was able to find some shapes that make up the entire shape of the Yin Yang. The entire shape is made of circles with varying diameters.
The shape has been divided into two half circles (red and blue) with equal diameters. Each of the diameters are equal to the radius of the larger circle.
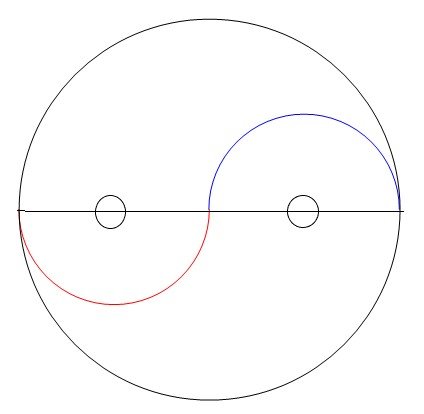
The final part of the construction is adding the two smaller circles contained in the shape. They are made by adding circles in the center of the smaller red and blue half circles.
Although in paint you can simply color it in, you can fill it in by adding half circles which gives a mesmerizing gif.
The Area

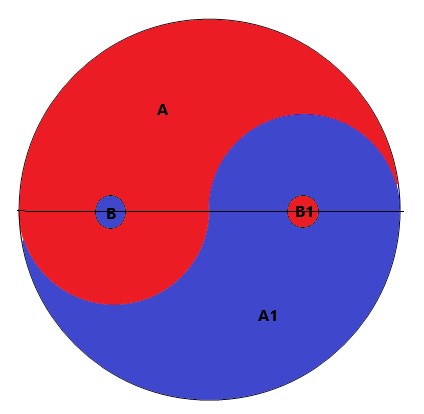
It's evident that each color is equally represented since every letter has a corresponding letter in the circle. So that means that the area of each color must be the same.
Quantitatively...
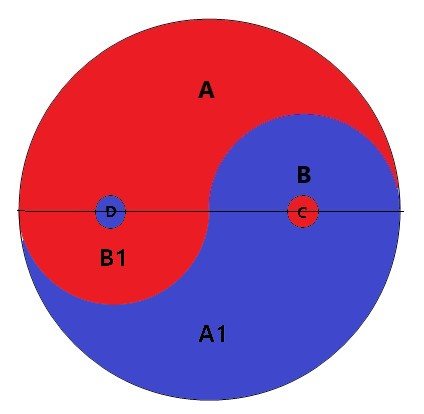
After I noticed to use the half of the HugeCircle I noticed that for both A1 and A, B1 cancels with B. In order to keep the equations as easy to calculate as possible they all only contain HugeCircle radius "R" and B1's circle radius R1. So for the calculation these are the equations to use.
Final thoughts
The construction is quite simple, all that is required is a compass and maybe a ruler. This construction can easily be a project for a geometry class in High School. There is something pure about a seemingly complicated shape being easy to make. The philosophical implications of such a shape are still used today. Even in the math the Yin Yang keeps it's philosophical identity of balance.