The Power Rule

---

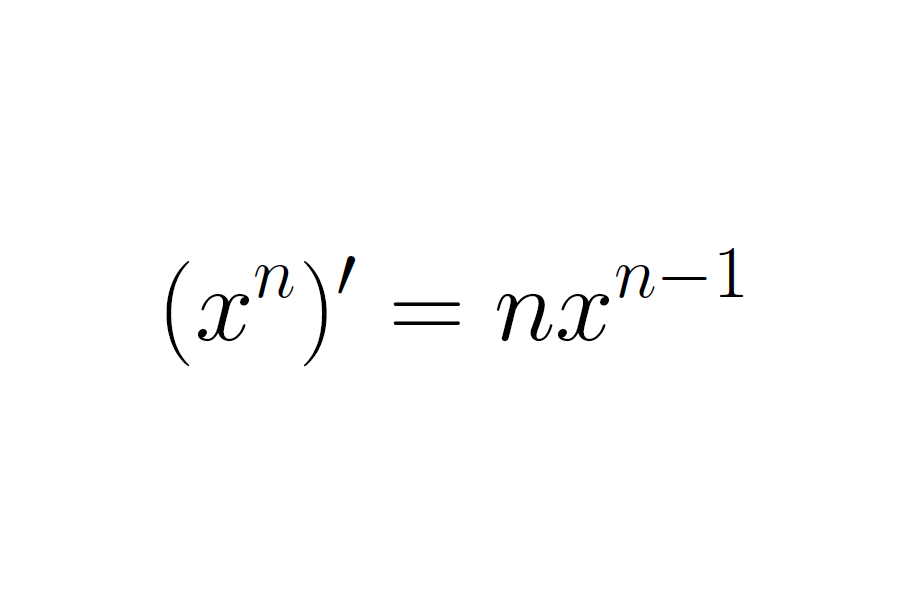
In calculus we can use the power rule to take the derivative of polynomial functions. The power rule is one of the simplest rules for finding derivatives and is usually the first rule learned by students in their study of calculus. The rule can be stated as follows:

---

Power Rule:

If f(x) = xⁿ then f'(x) = nx^{n - 1}.

---

The power rule tells us that to take the derivative of the function xⁿ we bring down the exponent n and then multiply by x to the power of n - 1. We usually work with the case that n is an integer but it is not necessary to assume that n is an integer. We can take n to be any real number and the power rule still holds. In the case n = 0 then we have f(x) = 1 and the power rule tells us that f'(x) = 0. This agrees with the fact that the derivative of a constant is equal to zero.

For our first example of the power rule we will calculate the derivative of the function f(x) = x². According to the power rule we have that f'(x) = 2x^{2 - 1} = 2x¹ = 2x. We can also find the derivative of f(x) = x⁵ using the power rule. In this case we have f'(x) = 5x^{5 - 1} = 5x⁴.

In the power rule we can also use negative values of n and the same process applies. Let us now find the derivative of the function f(x) = 1 / x. From the basic rules of exponents we know this function is the same as f(x) = x^-1. Once our function is in this form it is easy to see that the power rule applies and we have f'(x) = -1x^{-1 - 1} = -x^-2 = -1 / x².

Once we are more comfortable with the power rule we will not write out all the steps and details as was done above. Using the properties of derivatives and the power rule we can find the derivative of any polynomial function. Suppose now that f(x) = 3x² - x + 1. We can find the derivative of this function by applying the power rule to each term of this polynomial. We have that f'(x) = 6x - 1 + 0 = 6x - 1.

In this post we have discussed the power rule and have given several examples of how to use the power rule to calculate the derivative of polynomial functions. The power rule is a simple rule to use but it also has its limitations. Most functions are not in the form of a function given by the power rule so we will need to derive other tools to find derivatives of more complicated functions.

---

References:

https://en.wikipedia.org/wiki/Power_rule
http://mathworld.wolfram.com/PowerRule.html

---

All images in this post were created by myself using latex.