No solution! #2 - P vs NP Problem / 無解 #2 - P vs NP問題
Here comes the 2nd post of this series. We will look at the famous P vs NP problem in computer science this time!
這是「無解」系列的第二篇文章。這次我們會看看在計算機科學中有名的P vs NP問題!

Proposers of P vs NP Problem (Left: Professor Stephen Cook, Right: Professor Leonid Levin)
P vs NP問題提出者 (左: Professor Stephen Cook, 右: Professor Leonid Levin)
(Image 圖源: http://www.claymath.org/millennium-problems/p-vs-np-problem)
A history lesson 起源
The well-known P vs NP Problem was formulated by Prof. Stephen Cook and Prof. Leonid Levin in 1971. The Clay Mathematics Institute named the P vs NP Problem as one of the seven Millennium Prize Problems in 2000 (another Millennium Prize Problem, known as the Riemann Hypothesis, is briefly mentioned in my previous post). Anyone who is able to give a proof of whether P = NP can get a million-dollar prize!
著名的P vs NP問題是在1971年由Prof. Stephen Cook及Prof. Leonid Levin提出。克雷數學研究所在2000年將P vs NP問題納入為七條千禧年大獎難題之中的其中一條未能解決的問題(我在上一篇文章有簡略提過另一條千禧年大獎難題 --- 黎曼猜想)。任何人如果能解決其中一條千禧年大獎難題均可獲得一百萬美元獎金!
What is NP? 何謂NP?
Let's explain an NP problem using a simple example. Imagine there are 1,000 students in a high school. You have a complete list of friends for each student. That is, for any student, you know exactly who his / her friends are. Now the principal gives you a task: given a list of 100 students, check that if each student is a friend of every other. You can then quickly verify by using a simple algorithm. Roughly speaking, any yes-no problem that can be verified quickly given a proposed solution is known as an NP problem. NP is the collection of all NP problems. You may come up with a question: what is meant by "quickly". One second or one minute? I will state a more formal explanation of NP in the following but if you are not comfortable with the mathematical terms, you may treat "quick" as a reasonable computation time that is shorter than forever. If you insist to know the full name of NP, it stands for "non-deterministic polynomial time".
讓我用一個簡單的例子去說明甚麼是一個NP問題。假設一所學校有1,000個學生而且你知道每一個學生的所有朋友是誰。現在校長給你一個任務: 如果你有一張100個學生的名單,請確定一個條件: 「名單上面的每任何一位學生均是名單上面其餘學生的朋友」。事實上對於任何一張100人的名單,你也可以用一個簡單的算法去檢查這個條件是否成立。粗疏地說,對於一個「是/否」問題,如果你可以快捷地驗證任何一個假設答案,該問題則為一個「NP問題」。而NP則為所有NP問題的集合。現在你可能會問一條問題: 何謂「快捷」。接著我會寫一個比較正統的定義,但如果你對一些數學術語不是太熟悉,你也可以大概理解「快捷」為一個「可以接受」的時間。如果你有興趣知道的話,這是NP的全寫: non-deterministic polynomial time.
Definition of NP
NP is the collection of all yes-no problems where any proposed solutions can be verified in polynomial time (i.e. O(n^k) where n is the size of the problem and k is some constant) by a deterministic Turing machine.
What is P? 何謂P?
Let's get back to the previous example. Now, instead of asking you to check a given solution, the principal now requests you to find a 100-student list such that each student is a friend of every other. Now this problem is VERY HARD to solve. An obvious approach is to try all the combinations and stop when a candidate solution satisfies the condition. But the number of ways to draw 100 students from 1000 students is more than the number of atoms in the observable universe! In general, any decision problem which can be quickly solved is known as a P problem. P denotes the set of all P problems, where P again stands for polynomial time. Note that any P problem is also an NP problem. In other words, any problem that can be quickly solved can also be quickly verified. In mathematical terms, P is a subset of NP. A formal statement of the P set is shown below.
我們再一次看看剛才的例子。現在校長要你解決另一個難題。他要你找一張100人的名單,符合跟之前一樣的條件:「名單上面的任何一位學生均是名單上面其餘學生的朋友」。雖然問題看似差不多,但實際上是非常困難的。一個直接的解決方法是找出所有100個學生的組合直到找到一個符合條件的組合。但要知道,從1000個學生選出100個的組合數量,比可見宇宙的原子數量還要多! 一般而言,P問題是指一些可以快捷地解決的問題。而P就是所有P問題的集合 (P指的是"polynomial time")。注意所有P問題同時也是NP問題。換言之,一個可以快捷地解決的問題必然是可以快捷地驗證的。用數學術語說的話,即P是NP的子集。下面有一個比較正式的定義。
Definition of P
P is the collection of all yes-no problems which can be solved in polynomial time by a deterministic Turing machine.
The Clique Problem 分團問題
The above example is indeed an illustration of the famous clique problem. We can represent each student by a point on a blank paper. Then, if 2 students are friends of each other, we connect them using a line. We now have a large network on the paper. A clique is a smaller network such that any 2 points are connected by a line. The first task (NP problem) from the principal is thus equivalent to verifying whether a given smaller network with 100 points is a clique, while the second task (P problem) is to find a clique with 100 points from the whole network.
上述學校的例子其實是由著名的分團問題演化而成。我們可以用在白紙上畫一點來代表其中一個學生。如果兩個學生是朋友,那麼我們就把那兩點連在一起。現在我們在白紙上有一個很大的網絡。團是指一個小網絡中任何兩點都是連在一起的。這樣看來,校長的第一個難題(NP問題)就是要驗證一個有100點的小網絡是否一個團,而第二個問題(P問題)則是要從整個網絡中找出一個有100點的團。
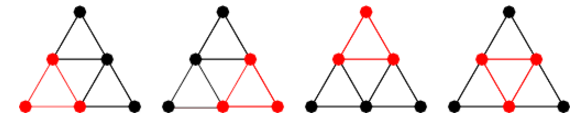
There are 4 cliques in the triangular graph above 上圖共有4個團
(Image 圖源: http://mathworld.wolfram.com/Clique.html)
The P vs NP Problem! P vs NP 問題
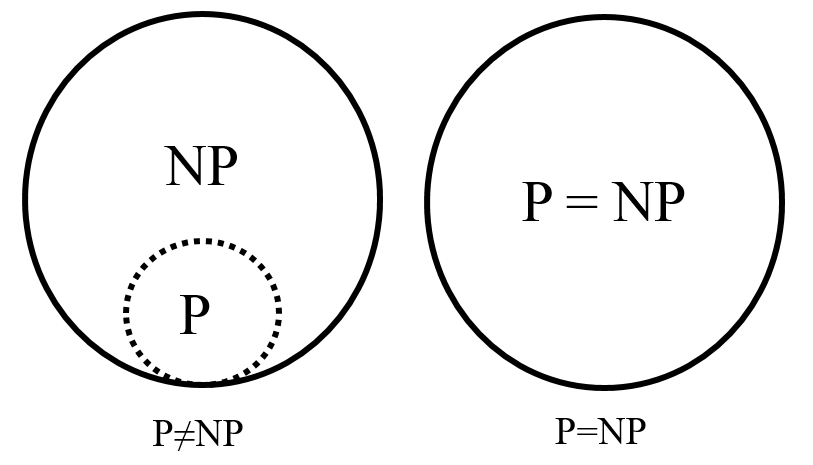
We discussed earlier that every P problem is also an NP problem. But how about its reverse? That is, is an NP problem also a P problem? Unfortunately, this problem remains unsolved and this is exactly the P vs NP problem, which is one of the seven Millennium Prize Problems.
我們之前提過所有P問題都是NP問題。那麼每條NP問題是否也是P問題? 這個問題暫時未有答案,而這正正就是七大千禧數學難題裡的P vs NP問題。
Why is that important? 為何要研究這個問題?
Assume P = NP, we know for sure that there must exist some algorithm to quickly solve the problem for any decision problem that can be quickly verified. If we are clever enough to find those algorithms, then our lives will be much easier. For example, some computational challenges related to DNA are NP problems. If P = NP, then incurable diseases such as cancer may have a way to cure. Yet P = NP will also cause troubles about cyber security especially regarding cryptography. According to a poll in 2012 by University of Rochester, only 17% of the respondents thought that P = NP.
如果P=NP, 那麼我們知道對於所有可以快捷地驗證的「是否」問題必然存在一些算法可以快捷地解決該問題。如果我們能夠找出那些算法,那麼很多難題便能得到解決。例如一些關於人類DNA的算法問題都是NP問題。如果P=NP,那麼一些絕症例如癌症便可能有治療的方法。但同時P=NP亦會製造其他問題,例如一般網絡保安上的加密法就會變得沒用。根據2012年羅切斯特大學的一個調查,只有百份之十七的受訪學者認為P=NP。
What's coming next? 下回預告
In the next post, we can explore more about some unsolved problems in geometry!
下次我們會看看一些幾何學上的未解問題!
References 參考
- SIGACT News Complexity Theory Column 74
- Wolfram Alpha
- Clay Mathematics Institute
- The Status of the P versus NP Problem
I write articles on machine learning, applied statistics, maths and economics to the best of my knowledge. If you like my posts, please upvote, resteem and follow me @manfredcml!
CN區的朋友大家好! 如果喜歡小弟的文章,可以upvote, resteem或follow @manfredcml支持!
English articles 英語文章:
Be a smart gambler! #1 - Gambler's fallacy
Let's play a game #1 - Prisoner's Dilemma
Paradox is fun! #1 - Boy or Girl?
No solution! #1 - Prime numbers
Everyday Tech Series
Bilingual articles 雙語文章:
Welcome to the world of mahjong! 歡迎來到麻雀教室! #1
Good one. You explained from the very basics and this one is much more easily understood by laymen than the prime number one imo. The bilingual feature of your article also makes it more outreaching to the prospective audience. Great efforts and continue upvoted for support. Maths is fun!
A great explanation on P and NP problem! it's very easy for users to understand. I guess P is not equal to NP as well, dun ask me why though, if I can prove it then I would have won the usd 1million prize!
Very good text. Keep it coming.
Thank you : )