Math challenge #3 - Find its length!
Question
(Difficulty: 2/10)
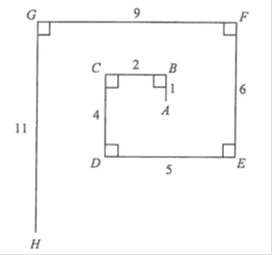
Find the length of the line segment AH.
This is actually a question from the latest public exam in Hong Kong (HKDSE, Hong Kong Diploma of Secondary Education Examination). See if you can pass the high school exam in Hong Kong! ;)
Solution
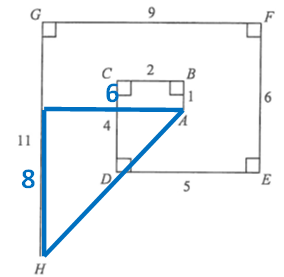
Thus by the Pythagoras' Theorem AH = 10.
(In case you have no idea about the Pythagoras' Theorem, it states that in a right-angled triangle, a^2 + b^2 = c^2, where c is the length of the longest side, a and b are the other two sides.)
Previous posts
Math challenge #1 - Find the remainder!
Math challenge #2 - Find the value of these recurring square roots
Excellent explanation! Very clear ;)
I got 10 as my answer and although I would share and show my work, I think that @mathfortress did it way better!
Glad that you get the answer! ;)
10, but I was too stupid to find that answer was posted after I calculated it.
It's not stupid at all, the process of solving a maths question is fun isn't it? ;)
yeah @helloworld123 has a point
great work on finding out the answer successfully!
the answer is 10...
(length(GF) - (Length(DE) - length(CB))) = 6
(length(GH) - length(FE) + length(CD) - length(AB) = 8
Root(88 + 66) = Root(100) = 10
Great!!!
Hi, I am the new curator for @math-trail, a community dedicated to promoting the best articles on mathematics in its widest sense, including educational and cultural aspects.
I just upvoted your post - hope to see more in the future.
If you like to write about mathematics, then please follow @math-trail and I will follow you back and look forward to see fresh new content.
If you enjoy reading about mathematics, then please follow me so that you will receive the best content in your personal feed.
I am not a bot! Thanks!