A pleasant day steemians ! Here I am again to do tutorials in algebra which is the laws of signed numbers. This topic is just so easy and I don't believe that you will not learn in this tutorial. So come on steemians, read and learn in this tutorials.

Image source

This are the following topics that I will discuss and I will also give a two or more samples in every topic.

• Addition of Signed Numbers
• Subtraction of Signed Numbers
• Multiplication of Signed Numbers
• Divisions of Signed Numbers
• Order of Operations

These are the five topics I will going to discuss but first, what is signed numbers ? Then where this numbers can be used ? So here's the answer for this two questions.

Signed numbers

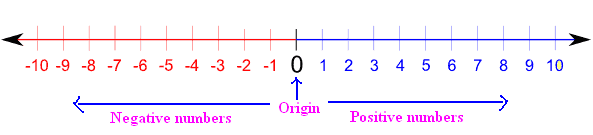
= it is a number with a plus sign (+) which is to indicate a positive quantity or by a minus sign (-) to indicate a negative quantity. There are two types of signed numbers. The positive number and the negative number.

Image source

• Positive number = it is numbers greater than zero which is in the right side or the numbers with a positive sign (+). The positive numbers with no sign of (+) is also consider a positive number.
• Negative number = the numbers that are less than zero which is in the left side of the picture or the numbers with a negative sing (-). The negative numbers is always has a negative sign (-) unlike in the positive numbers can be without a positive sign (+).

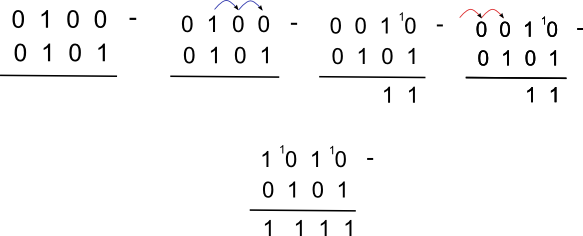
Image source
In arithmetic you can't subtract smaller number togreeater number or you can't subtract if the first number is greater than the second number. Just like in the photo above. The zero subtract to one but in able to get the answer they will the borrowing method. But here in algebra we can do the subtracting even if the first number is smaller than the second number. We have four operations in doing the calculations and each operation has a different rules. We will start with the first now.

Addition of Signed Numbers

Rules in Adding Signed Numbers :

• To add two numbers having like signs or the same signs (+ and + or - and -), find the sum of their absolute value (values of a number regardless of the sign) and the prefix the common sign.

• To add numbers having unlike signs or different signs (+ and - or - and +), find the difference of their absolute values and prefix the sign of the number with greater absolute values.

Example :

• Find the sum of -8 + (-5).

1st step

You will look their signs and if their the same you will just copy the sign to the result of their sum. So their signs are negative (-).

2nd step

You will add the two values which is the 8 and 5 and their result is 13.

last step

So the answer is negative 13 (-13).
-8 + (-5) = -13

• Find the sum of -26 + 8.

1st step

Look at their signs and in this case the signs are unlike or different (- and +) so you will find which number is the greater value and what sign of that greater number has. The greater number of this problem is 26 and it is a negative sign (-) so the result of their sum must be negative sign (-) but if the greater number is positive the result of their sum is also positive.

2nd step

You will find their difference because they are unlike signs (26 -8) so their difference is18.

last step

So the result of their sum is negative 18 (-18).
-26 + 8 = -18

Subtraction of Signed Numbers

Rules for Subtraction of Signed Numbers

• To subtract one number from another, first change the sign of the number being subtracted and then add. If a and b is a real number, then
  a - b = a + (-b) or a + b = a - (-b)

Example :

• Find the difference of 8 - (-2).

1st step

You will look at first their signs and in this case it is look like the rule that if a - (-b) it is equal to a + b so it will be like this now 8 + 2.

2nd step

You will add now the the two real numbers because it is addition now because of the rule if a - (-b) = a + b.

last step

The result of this problem is positive 10 (+10 or 10).
8 - (-2) = 8 + 2 = 10

• Find the difference of -6 + (-3).

1st step

You will look first what kind of rule you are going to use and in this problem it is like the rule that if a + (-b) is equal to a - b. Don't mind the sign of the first number and just don't change the sign of the first number even if it is positive (+) or negative (-). So this problem will become -6 - 3.

2nd step

The two numbers has a like signs or the same signs so in this case we will use the rule of addition which is if it is like signs you will add the two numbers and copy their sign to the result of their sum.

last step

The result of this problem now is negative 9 (-9).
-6 + (-3) = -9

• Find the difference of 3 + (-1.5).

1st step

So in this problem we already picture out what kind of rule we were goig to use and it is the a + (-b) = a - b. This problem will be like this now 3 - 1.5 .

2nd step

Their signs are unlike so we know in the rule of addition, we will find the difference of the two numbers if they are unlike signs. Then in the rule of addition you will find what is the sign of the greater number and in this problem the greater number is 3 and its sign is positive (+). So the result of their difference will be also a positive sign.

last step

The result of their difference is positive 1.5 .
3 + (-1.5) = 1.5

Multiplication of Signed Numbers

Rules in Multiplication of Signed Numbers

• To find the product of two signed numbers, multiply their absolute values. If the numbers have like signs, the product is positive. If they have unlike signs or different signs, the product is negative.

• To know that the operation to use is multiplication, it must be like this "(a)(b)" or "a * b". The sign like this "x" in multiplication is only in arithmetic because here in algebra the x represents as variable.

• Just follow this rule. If (-)(-) = + , (+)(+) = + , (-)(+) = - , (+)(-) = - .

Example:

• Multiply (-8)(-9)

1st step

You will look first if the signs are like or the same and in this case the signs are the same so the result of this problem or the product of this problem will be positive (+) because they have like signs. If the signs of the two numbers are different or unlike, the answer or the product will be negative (-) because they are unlike. In our 1st problem the product will be positive (+) because they are like signs.

2nd step

You will multiply the two numbers and you will get the product.

last step

The product of this problem is positive 72.
(-8)(-9) = 72

• Multiply (-4)(-5)(-2)

1st step

In this problem there are three numbers, so 1st thing you will do is you must find the product of the first and second number because they need to be in order. The first and second number are like signs, so the product will be positive (+).

2nd step

The product of the first and second number is positive 20 so the new problem now is "(20)(-2)" and as you can see their signs are unlike so if we will get the product of the this two number the result will be negative because unlike signs is negative.

last step

The product and the final answer now is negative 40 (-40).
(-4)(-5)(-2) = (20)(-2) = -40

Division of Signed Numbers

Rules in Division of Signed Numbers

• To find the quotient of two signed numbers, find the quotient of their absolute values. If the numbers have like signs, the quotient is positive. If they have unlike signs, the quotient is negative.

• Just follow this rule. If (-) ÷ (-) = + , (+) ÷ (+) = + , (-) ÷ (+) = - , (+) ÷ (-) = -.

• If the presentation is like this "a / b" or "a ÷ b" then we can say that it is a division.

Example :

• Simplify (-8) ÷ (-4)

1st step
The division is just the same in the multiplication so in this problem they have the same signs of negative (-) and as stated in the rule that if the two numbers is like signs then their quotient is positive (+).

2nd step

You will going to divide the two numbers and their result is positive.

last step

The quotient of this two number is positive 2.
(-8) ÷ (-4) = 2

• Simplify (-10) ÷ (2)

1st step

The two numbers has different signs so if they are unlike signs the quotient must be negative (-). So in this problem the quotient will be negative.

2nd step

Divide the two numbers and you will get the quotient of this problem.

last step

The quotient is negative 5 (-5).
(-10) ÷ (2) = -5

Order of Operations

Rules of Order of Operations

• Carry out all operations within symbols of grouping, working from the innermost symbols outward.

• Carry out all multiplications and divisions, working from left to right.

• Carry out all multiplications and subtractions, working from left to right.

• Use the method PMDAS (Parenthesis, Multiplication, Division, Addition, Subtraction) which you will do the operation first inside the parenthesis then the next operation you will do is multiplication and followed by division and addition and the last is subtraction. But the division and addition can be interchange because it depends on the problem. The divisor and dividend must be a one number only in each of them to operate the division.

note : The most common symbols of grouping are the parentheses (), brackets [] and the braces {}.

We will be going to solve a little tricky problem because we will use the four operations with the order of operations in one problem. So here we go let's solve and learn this kind of problem.

• Simplify 4(8 + 3) - 9

1st step

We will going to use the PMDAS method and the first operation we will do is inside the parentheses.
4(8 + 3) - 9 = 4(11) - 9

2nd step

We will do now the next step in the method of PMDAS which is the multiplication. So in our problem 4(11) is multiplication and their signs are the same so their product will be positive.
4(11) - 9 = 44 - 9

last step

In our new form of problem we can't see a division and addition because it is already subtraction "44 - 9". So we know in the subtraction, we will subtract the two numbers and find out the sign of the greater number. In our problem the sign of the greater number is positive so their difference will be positive (+). Then we will get our final answer positive 35.
4(8 + 3) - 9 = 4(11) -9 = 44 -9 = 35.

• Simplify 5(-3 - 2) + (-5 + 2) / 2(-8) + 12

1st step

We will the PMDAS again and it's gonna be a little tricky because we will be using all methods. So the first is parentheses. We will do the operation first inside the parentheses which is the (-3 -2) and the (-5 + 2). In the first parentheses, their signs are like so we will add them and their signs is negative (-) then the result of their sum is negative. The 2nd parentheses are unlike sign so we will subtract them and the result of their difference is negative (-) the greater number has a negative sign.
5(-3 - 2) + (-5 + 2) / 2(-8) + 12 = 5(-5) + (-3) / 2(-8) + 12

2nd step

The next operation is multiplication so we will multiply the following numbers, "5(-5)" and "2(-8)" so we know that in multiplication if they are unlike signs their product will be negative (-).
-25 - 3 / -16 + 12

3rd step

Actually the next operation is division but we can't divide this "-25 - 3 / -16 + 12" because the divisor and dividend are not one number in each so we must do the addition in "-25 - 3" and subtraction in "-16 + 12" first. So the the first two numbers are like sign so they are addition and their result is negative (-). Then in the second two numbers they are unlike sign so they are subtraction and their result is negative (-) because the sign of the greater number is negative.
-28 / -4

Last step

We will do now the division because the divisor is already a one number and also in dividend. The final answer is positive 7 because they are like signs and as stated in the rule of division, if they are like sign the quotient will be positive.
5(-3 - 2) + (-5 + 2) / 2(-8) + 12
= 5(-5) + (-3) / 2(-8) + 12
= -25 - 3 / -16 + 12
= -28 / -4
= 7

That's all for my tutorials now I hope you enjoy reading this tutorial and I also hope you learn something from this tutorial. Thank you so much for taking time to read this blog and thank you so much to all steemians. Have a nice day and I hope you all doing great.

Thanks and Godbless
@jumargachomiano