El universo según Emmy Noether

En 1915, dos de los principales matemáticos del mundo, David Hilbert y Felix Klein, invitaron a Emmy Noether a la Universidad de Göttingen para investigar un rompecabezas. Había surgido un problema en la nueva teoría de la gravedad de Albert Einstein, la relatividad general, que había sido revelada a principios de año. Parecía que la teoría no se apegaba a un principio físico bien establecido conocido como conservación de la energía, que establece que la energía puede cambiar las formas pero que nunca puede ser destruida. Se supone que la energía total permanece constante. Noether, una joven matemática sin una cita académica formal, aceptó con gusto el desafío.

Ella resolvió el problema de frente, mostrando que la energía no puede conservarse "localmente", es decir, en un espacio arbitrariamente pequeño, pero todo funciona cuando el espacio es suficientemente grande. Ese fue uno de los dos teoremas que probó ese año en Göttingen, Alemania. El otro teorema, que en última instancia tendría un impacto mucho mayor, descubrió un vínculo íntimo entre las leyes de conservación (como la conservación de la energía) y las simetrías de la naturaleza, una conexión que los físicos han explotado desde entonces. Hoy en día, nuestra comprensión actual del mundo físico, desde partículas subatómicas hasta agujeros negros, se basa en gran medida en este teorema, ahora conocido simplemente como el teorema de Noether.

"Es difícil exagerar la importancia del trabajo de Noether en la física moderna", dijo la física de la Universidad de Durham Ruth Gregory un siglo después. "Sus conocimientos básicos de simetría son la base de nuestros métodos, nuestras teorías y nuestra intuición. El vínculo entre la simetría y la conservación es cómo describimos nuestro mundo ".

Una vida de trabajo

¿Quién era esta mujer, invocada por dos renombrados matemáticos para ayudar a rescatar la obra maestra de Einstein? A primera vista, Noether (pronunciado NUR-tuh) parece haber sido una curiosa elección. Ella no tenía un trabajo real en matemáticas y apenas podía obtener una educación en el campo. Sin embargo, ella había publicado algunos documentos importantes, y Hilbert sentía que su experiencia podría ayudar a aclarar el problema con la relatividad general.

Nacido en Erlangen, Alemania, en 1882, Noether esperaba seguir los pasos de su padre matemático, Max. Pero las universidades alemanas no admitieron a las mujeres cuando llegó a la edad universitaria, por lo que Noether tuvo que auditar las clases en su lugar. Eventualmente ella lo hizo tan bien en los exámenes finales que obtuvo una licenciatura.

En 1904 se le permitió inscribirse en un programa de doctorado en la Universidad de Erlangen. Ella recibió un Ph.D. en 1907 y pasó casi ocho años trabajando allí sin sueldo o en un puesto oficial, confiando en su familia para obtener apoyo financiero mientras que de vez en cuando reemplazaba a su padre como maestra sustituta. Después de su viaje a Göttingen en 1915, se quedó como conferenciante, nuevamente sin recibir pago.

Después de años de trabajar esencialmente como voluntaria, Noether finalmente se convirtió en profesora asociada de matemática no unida en 1922 en Göttingen, donde se le asignó un modesto salario. Pero 11 años después, perdió su trabajo cuando ella y otros judíos fueron expulsados ​​de la academia en la Alemania nazi. Poco después, ella dejó el país y consiguió un trabajo en Bryn Mawr College en Pennsylvania, con la ayuda de Einstein. Murió apenas 18 meses después debido a complicaciones de la cirugía para extirpar un quiste ovárico.

Conservación de momento

En sus 53 años, muchos pasaron eludiendo un sistema que le impidió su búsqueda de las matemáticas, Noether tuvo un impacto extraordinario tanto en el álgebra (su campo principal) como en la física. No se sabe qué más podría haber logrado si la sociedad y el destino hubieran sido más amables. Sin embargo, su cuerpo de trabajo era más que suficiente para asegurar su lugar en el panteón de grandes científicos, con su teorema homónimo tal vez su contribución más duradera.

El espesor del teorema

El teorema de Noether es un vínculo simple y elegante entre conceptos aparentemente no relacionados que, hoy en día, es casi obvio para los físicos. Pero los no físicos también pueden entenderlo.

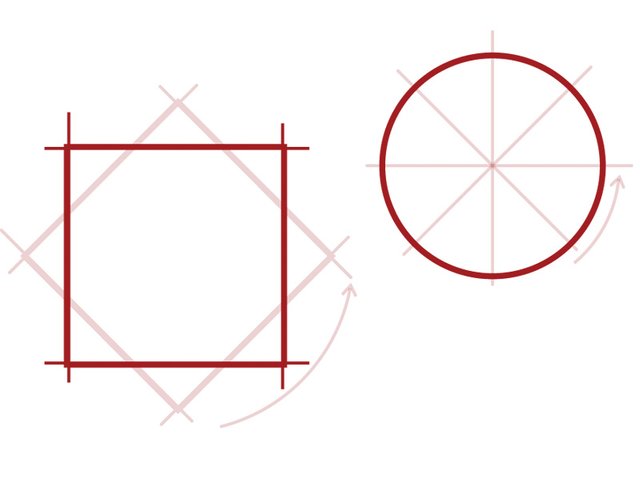
Básicamente, establece que cada simetría "continua" en la naturaleza tiene una ley de conservación correspondiente, y viceversa. Vamos a desglosar algunos de esos términos. La simetría, en este contexto, se refiere a una operación que se puede hacer a un objeto o sistema que la deja sin cambios. Girar un cuadrado 90 grados es un ejemplo de simetría "discreta". El cuadrado todavía se ve igual, mientras que una rotación de 45 grados produce algo diferente (comúnmente llamado diamante). Un círculo, por otro lado, posee una simetría continua ya que rotarlo en cualquier grado, o una fracción del mismo, no altera su apariencia. Este es el tipo de simetría al que se aplica el teorema de Noether. Una ley de conservación, por su parte, se refiere a una cantidad física que permanece fija y por lo tanto no fluctúa con el tiempo. La energía, por ejemplo, no puede ser creada o destruida; una vez que haya calculado su valor, no hay necesidad de repetir el cálculo.

Simetría

El teorema de Noether descubrió una relación oculta entre dos conceptos básicos: simetrías y cantidades conservadas, que hasta entonces habían sido tratados por separado. El teorema proporciona una fórmula matemática explícita para encontrar la simetría que subyace a una ley de conservación dada y, a la inversa, encontrar la ley de conservación que corresponde a una simetría dada.

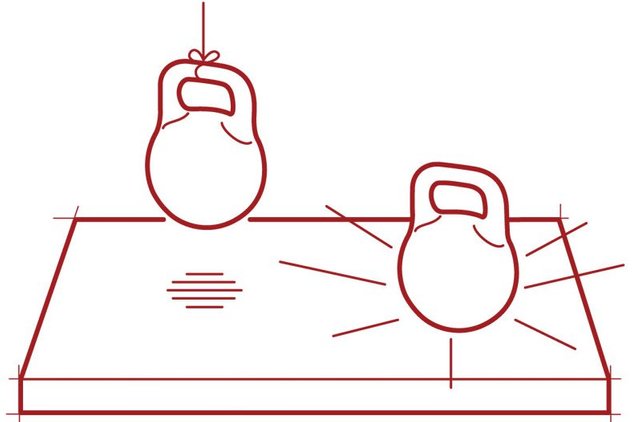
Aquí hay un vistazo al teorema en acción: imagine un disco de hockey deslizándose a lo largo de una lámina de hielo perfectamente lisa, sin fin y sin fricción. Supongamos además que no hay fuerzas externas actuando sobre el disco en absoluto. Bajo estas condiciones idealizadas, el disco continuará deslizándose en línea recta sin disminuir la velocidad. Su impulso, el producto de su masa y velocidad, será retenido o conservado. Lo único que podría hacer que el disco alterne su curso, o que gane o pierda velocidad, sería si el espacio mismo (la superficie del hielo, en este caso) variara. Sin embargo, nada cambiará si el hielo permanece liso y el espacio permanece sin cambios.

Simetría

El teorema de Noether descubrió una relación oculta entre dos conceptos básicos: simetrías y cantidades conservadas, que hasta entonces habían sido tratados por separado. El teorema proporciona una fórmula matemática explícita para encontrar la simetría que subyace a una ley de conservación dada y, a la inversa, encontrar la ley de conservación que corresponde a una simetría dada.

Aquí hay un vistazo al teorema en acción: imagine un disco de hockey deslizándose a lo largo de una lámina de hielo perfectamente lisa, sin fin y sin fricción. Supongamos además que no hay fuerzas externas actuando sobre el disco en absoluto. Bajo estas condiciones idealizadas, el disco continuará deslizándose en línea recta sin disminuir la velocidad. Su impulso, el producto de su masa y velocidad, será retenido o conservado. Lo único que podría hacer que el disco alterne su curso, o que gane o pierda velocidad, sería si el espacio mismo (la superficie del hielo, en este caso) variara. Sin embargo, nada cambiará si el hielo permanece liso y el espacio permanece sin cambios.

Conservación del momento angular

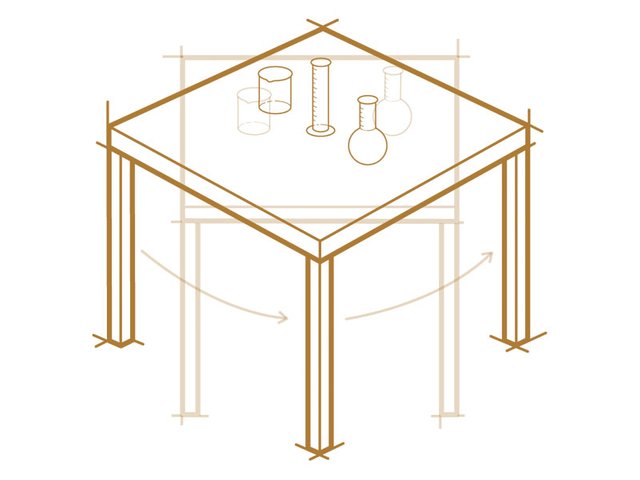
El teorema de Noether muestra que la conservación del momento del disco está vinculada a su "simetría de traducción espacial", que es otra forma de decir que la física no se ve afectada por movimientos (o traducciones) lineales dentro de un espacio uniforme. El disco se mueve de la misma manera en una parte del hielo liso que en otra.

De manera similar, el teorema de Noether muestra que la simetría bajo rotación, o la invariancia rotacional, conduce a la conservación del momento angular, que mide cuánto rota un objeto. La física, en otras palabras, no tiene una dirección preferida. Si haces un experimento en una mesa y luego giras esa tabla en 45 grados, o de hecho en cualquier cantidad, los resultados experimentales no serán diferentes. El teorema también vincula la simetría de la "traducción del tiempo" con la conservación de la energía, por lo que a la física tampoco le importa si haces un experimento hoy, el próximo martes o el tercer domingo de octubre.

Los físicos sabían sobre la conservación del impulso, el momento angular y la energía mucho antes de que apareciera el teorema de Noether. Son los preceptos fundamentales de la mecánica clásica. Pero no se sabía que estas leyes sagradas compartían un origen común, cada una ligada a una simetría particular. Esta nueva idea, que surgió del trabajo de Noether, es un principio rector que impregna la investigación de la física, al tiempo que informa nuestras visiones del universo en general....

Conservación de la Energia

Poniendolo todo junto

El teorema de Noether se aplica no solo a estas simetrías intuitivas (rotaciones y cambios en el tiempo o el espacio) sino también a simetrías "internas" más abstractas que subyacen a las fuerzas de la naturaleza.

Por ejemplo, la conservación de la carga eléctrica, un principio central de la teoría del electromagnetismo, surge de una simetría relacionada con los detalles del giro de la partícula. Otro ejemplo: una simetría llamada isospin que permite sustituir electrones por neutrinos y neutrinos por electrones, ayudó a los físicos a desarrollar una teoría en los años 60 que unificaba la fuerza electromagnética y la fuerza débil (que explica las desintegraciones de partículas y los procesos radiactivos) en un solo fuerza electrodébil. La cantidad conservada aquí es "hipercarga" - un tipo de carga, análoga a la carga eléctrica, que está asociada con esta fuerza electrodébil. Una década más tarde, los físicos idearon una teoría para la fuerza nuclear fuerte, que une protones y neutrones en el núcleo atómico. En el corazón de esta fuerza se encuentra algo llamado simetría de color. (El color es una propiedad de los quarks que forman protones y neutrones, que los físicos ven como otro tipo de carga).

En la década de 1970, los físicos clasificaron todas las partículas conocidas (incluidas algunas cuya existencia aún no se había confirmado, como el bosón de Higgs) y las fuerzas que gobiernan sus interacciones (electromagnética, débil y fuerte) en un único marco teórico conocido como el Modelo estandar.

Según el físico de la Universidad de Stanford Michael Peskin, el teorema de Noether fue una herramienta básica en la construcción de este modelo increíblemente exitoso. "En la mecánica cuántica, identifica dos o tres partículas que se supone que están vinculadas por una simetría y luego ve si la ley de conservación inferida es válida. Así es como aprendes si se trata de una verdadera simetría de la naturaleza, y así fue como se construyó el Modelo Estándar "- a través de un proceso acumulativo paso a paso como este. También es la forma en que los investigadores están tratando de avanzara

Un Súper Legado

La búsqueda continúa para encontrar nuevas partículas y simetrías más profundas y amplias a partir de las cuales surgen, un proceso en el que el teorema de Noether sigue desempeñando un papel fundamental. Gran parte del esfuerzo actual se centra en buscar signos de supersimetría, una teoría que postula una simetría entre las partículas que componen la materia (fermiones) y las partículas que transmiten fuerzas, como el electromagnetismo (bosones). Si la supersimetría es correcta, cada fermión conocido tiene un "supercompañero" bosónico por observar, y cada bosón conocido, de la misma manera, tiene un súper compañero fermiónico aún no visto.

Las hipotéticas partículas supersimétricas, que los físicos esperan descubrir en aceleradores de partículas gigantes como el Gran Colisionador de Hadrones, serían "un reflejo de todas las partículas del Modelo Estándar, utilizando un espejo ligeramente distorsionado", explica Joseph Incandela, físico de la Universidad. de California, Santa Barbara. "Las partículas en el otro lado del espejo se parecen a las partículas del Modelo Estándar, excepto que sus giros han sido ligeramente desplazados".

Supersimetría

Una posibilidad que se ha asociado con esta simetría supuesta, dice Incandela, es la conservación de algo llamado r paridad, lo que implica que la partícula supersimétrica más liviana debe ser estable y nunca puede descomponerse. Si efectivamente se conserva la paridad r, la pareja supersimétrica invisible de cada partícula ordinaria eventualmente se descompondrá en la partícula supersimétrica más liviana, que se queda para siempre. Esa partícula, cualquiera que sea, estaría disponible en cantidades abundantes y podría ser un buen candidato para la misteriosa materia oscura que se cree que representa más de una cuarta parte de las cosas en el universo.

Iluminando agujeros negros

Paradoja del hoyo negro de información

El teorema de Noether, sin embargo, es crucial para algo más que la simple búsqueda de nuevas partículas; se extiende a todas las ramas de la física. El físico de Harvard Andrew Strominger, por ejemplo, ha identificado un número infinito de simetrías relacionadas con partículas blandas, que son partículas que no tienen energía. Estas partículas vienen en dos variedades: fotones blandos (partículas que transmiten la fuerza electromagnética) y gravitones blandos (partículas que transmiten la fuerza gravitacional). Recientes trabajos de Strominger y sus colegas, Stephen Hawking y Malcolm Perry de la Universidad de Cambridge, sugieren que el material que cae en un agujero negro agrega partículas blandas al límite del agujero negro, o horizonte de eventos. Estas partículas en efecto servirían como dispositivos de grabación que almacenan información, proporcionando pistas sobre el material original que entró en el agujero negro.
La idea propuesta por los tres físicos ofrece una nueva estrategia para abordar un acertijo de larga data en la física conocido como la paradoja de la información del agujero negro. Hawking demostró en la década de 1970 que cada agujero negro eventualmente se evaporaría y desaparecería, potencialmente destruyendo toda la información que el objeto alguna vez contenía sobre cómo se formó y evolucionó con el tiempo. La pérdida permanente de información en el escenario de Hawking fue preocupante para los teóricos, incluido Hawking, ya que violaría una ley apreciada de la física cuántica que sostiene que la información, como la energía, siempre se conserva.
La presencia de partículas blandas a lo largo del horizonte de sucesos y sus simetrías correspondientes pueden apuntar hacia una salida a este dilema. "Rápidamente nos dimos cuenta por medio del teorema de Noether de que había leyes de conservación correspondientes a las nuevas simetrías que imponen restricciones muy estrictas a la formación y evaporación de los agujeros negros", dice Strominger, aunque reconoce que este trabajo aún se encuentra en una etapa inicial.
Es solo un escenario más en el que el teorema de Noether se ve grande, y la lista de ejemplos sigue creciendo. "La relación entre las simetrías y las leyes de conservación es una historia interminable", dice Strominger. "Cien años después, el teorema de Noether sigue encontrando más y más aplicaciones".

Si bien nadie sabe qué vendrá después, el poder increíble y la longevidad del teorema de Emmy Noether son innegables.