¿Cómo dividir 2 entre 1/2? (TUTORIAL). Parte II
Este pequeño tutorial para explicar uno de los casos de la división de fracciones, no pretende en modo alguno sustituir la información que a este respecto aparece en cualquier libro de matemática, más bien se presenta como alternativa para vincular el conocimiento con la realidad del estudiante, y sus vivencias, de tal manera que pueda servir; como apoyo en el ejercicio didáctico de la enseñanza referida a este contenido en particular. De allí que no se presente la formalización matemática inherente al mismo.
Está basado en mi experiencia como docente del área, a nivel de secundaria y en la teoría del aprendizaje significativo de David Ausubel, que hace énfasis en la conexión de los conocimientos previos con la nueva información, en el marco de la psicología constructivista.
En nuestra primera entrega, se abordó mediante algunos ejemplos contextualizados con el entorno del estudiante, la forma de dividir ½ entre 2, que aplica para dividir una fracción propia entre un entero. En esta oportunidad se pretende ilustrar la forma de dividir 2 entre un medio, esto es, el proceso contrario.
¿Cuánto es 2 dividido entre ½?
La respuesta a esta interrogante conduce a su vez a preguntarnos:
¿Cuántas veces cabe ½ en dos unidades?
¿Cuántas veces 2 contiene a ½?
¿Cuántas mitades caben en 2 unidades?
Y esta situación, puede ser contextualizada de la siguiente manera:
¿Cuántas veces cabe la mitad de una taza de chocolate, en un recipiente que contiene 2 tazas?
¿Cuántas medias tazas de chocolate se requieren para llenar un recipiente que contiene 2 tazas?
Con dos medias tazas lleno hasta la mitad, el recipiente dado; esto es, completo una taza. Con dos tazas adicionales completo la totalidad del recipiente. Es decir, necesito cuatro medias tazas para llenar el recipiente.
En este contexto, dos dividido por un medio, representa cuatro mitades. Cuatro medias partes.
Cada unidad tiene dos mitades, por lo tanto dos unidades representan 4 mitades.
Otro ejemplo relacionado con nuestro quehacer diario, pudiera ser: ¿Cuántos medios litros de leche necesito para completar 2 litros?
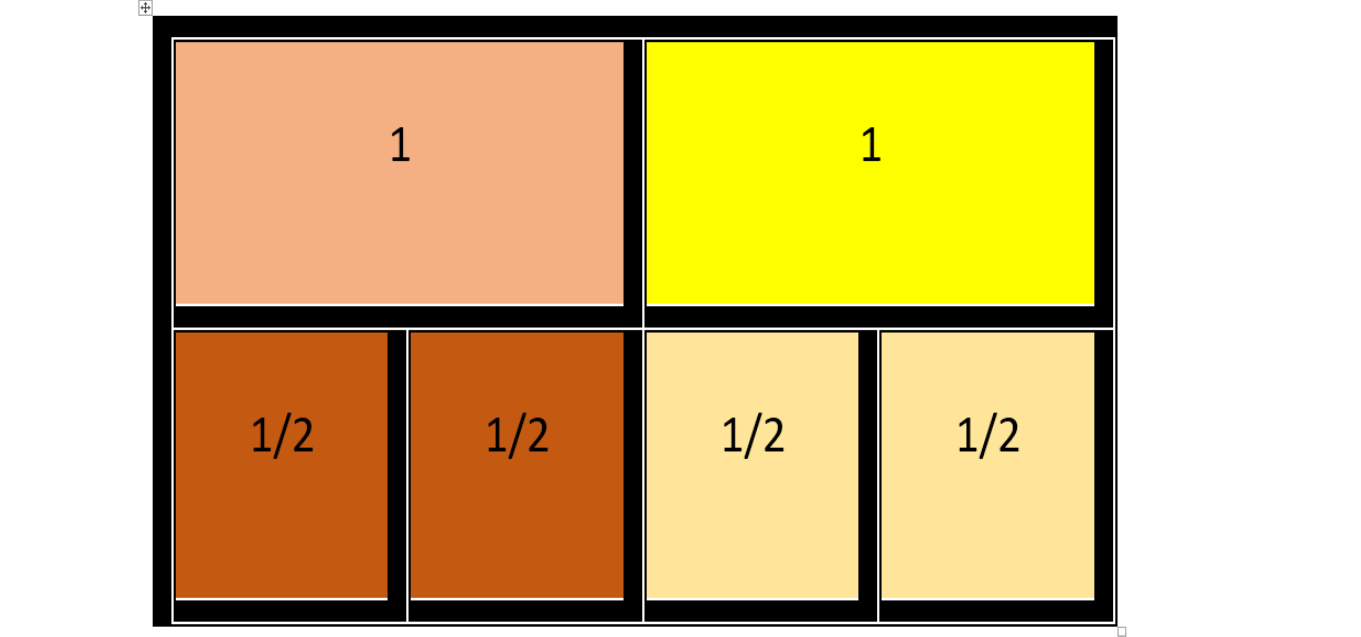
Gráficamente: En la figura adjunta, se observan 2 rectángulos en la parte superior y en la parte inferior se muestra cada uno de los rectángulos anteriores dividido en dos partes iguales. Nótese que a cada rectángulo de arriba le corresponden dos rectángulos abajo.
Al dibujar un rectángulo a continuación del otro, se puede ver que en los dos rectángulos caben 4 mitades.
Luego, 2 dividido por un medio es igual a 4.
REFERENCIAS BIBLIOGRAFICAS
Teoría del Aprendizaje Siginificativo. David Ausubel
Planificación de contenidos para 1er año de Educación Básica. Higinio Villalobos. Maracaibo. Venezuela.