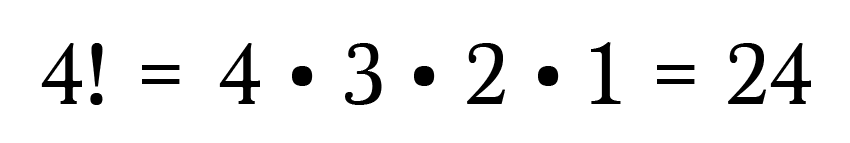What Is A Factorial and How Are Factorials Used In Statistics?
The factorial of a number is the product of the integers from the number down to one. Factorials are used in probability, combinations, and permutations.
The factorial function is one of the most important in statistics and probability. The function is written as n! (pronounced n-shriek, n-bang, or n-factorial) and the Excel math function used to calculate it is FACT(). e.g. FACT(4) will return the value 24.
Factorial Function Definition
For a positive integer (whole number), n, it is defined as one times two times three … times n-1 times n. For instance
4! = 4 × 3 × 2 × 1
= 24
The factorial function is not defined for negative numbers. The function is defined for zero, where by convention
0! = 1
The Excel and JMP / SAS Factorial Functions
The Microsoft Excel function FACT() returns the value of the factorial of the number inside the brackets. It is very convenient and easy to use, although the function needs to be used carefully. For example, the Excel command
=FACT(4.5)
will return the number 24, as will
=FACT(4.99).
In other words, Excel rounds down the number in brackets before doing the calculation. This may cause errors when the number in brackets is a value that has been calculated, and an "almost integer" is given to the function.
Factorial numbers become large very quickly, and the highest number that Excel can calculate the factorial of is only 170. FACT(170) is about 7.3 × 10^306, larger than the number seven followed by 305 zeros.
The SAS / JMP function format is
Factorial(:X) where X is the column name. Like Excel, the maximum number for which it may be calculated is 170. The factorial function may be found in the list of "Transcendental" functions.
Factorial Function Uses
Factorial functions are used throughout statistics and probability. For example, the number of ways that n articles may be arranged is n!, or to calculate the odds of winning the UK national Lottery, by picking six numbers from forty-nine, the odds are one in
49! / 6!. (49-6)!
=49! / (6! × 43!)
Factorials are also used throughout mathematics: the sine of an angle θ radians is given by the formula
sine(θ) = θ - θ^3/3! + θ^5/5! - θ^7/7! + ...
and the number e, the base of natural logarithms, is the sum of
1 + 1/1! + 1/2! + 1/3! + ...
Estimating Factorials Of Large Numbers
Sometimes a formula uses the factorial function, but the software being used cannot provide the answer. Excel , for example, will return the error #NUM if the user tries to calculate factorial 171 or higher. The user has a few options. First, it is sometimes possible to "cancel out" or simplify a formula. For example
172! ÷ 171! = 172.
There are also some formulas used to estimate n! The best known is Stirling's formula
n! ~ √(2.π.n) × (n / e)^n
where e is the base of natural logarithms, or 2.71828...
This formula is a reasonable estimate, but Ramanujan gave the more accurate estimate
log(n!) ~ n.log(n) - n +log(√π) +log(n + 4n² + 8n³)/6
When dealing with large values of n, both formulas listed become more accurate.
Factorial Function Summary
The factorial function is one of the most useful in mathematics and statistics, especially when calculating combinations and permutations. It may be calculated for any positive integer n and zero, although it becomes large very quickly as n increases. Formulas exist to estimate n! when n is large.
Factorial Function References
Abramowitz, M. & Stegun, I., Handbook of Mathematical Functions, US Department of Commerce
Ramanujan, Srinivasa, The lost notebook and other unpublished papers, Springer Berlin