Geometric Progression Math Formulas - Derivation and Usage

Geometric progressions are a series of numbers, where each term is a fixed number times the previous term. This article discusses the formulas and their use

A geometric progression is a series of numbers, each one differing from the previous number in the series by a common ratio. There are two common formulas associated with geometric progressions. The first is the formula for the "n"th term (e.g. the sixth term) in the series, and the other is the formula to sum the series from the "n"th to the "m"th (e.g. sum the series from the third number in the series to the tenth.)

source

Geometric Progressions - Examples and Definitions

Example 1: 1, 10, 100, 1000, 10000, …

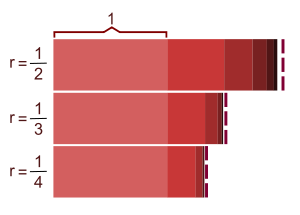
Example 2: 2, 1, 0.5, 0.25, …

Example 3: -2, 2, -2, 2, -2 …

The first term is often designated as "a", and the common ratio is usually referred to as "r". In the three examples shown, the values for "a" and "r" are:

Example 1: a = 1, r = 10

Example 2: a = 2, r = 0.5

Example 3: a = -2, r = -1

Geometric Progression Formulas For "n"th Term and Sum on n Terms

The formula for the "n"th term is easily derived. The first term equals "a", by definition. The second term is equal to a × r, the third term is a × r², the third term is a × r³. In general, the "n"th term is a × r to the power of (n - 1).

To derive the formula for the sum of the first "n" terms, a little algebra is needed. Let the sum of the the first "n" terms = S:

S = a + a.r + a.r² + a.r³ + ... + a.r^(n-1) [Equation 1]

Now multiply each side of the equation by r:

S.r = a.r + a.r² + a.r³ +... + a.r^(n) [Equation 2]

Now subtract Equation 1 from Equation 2: [Note that the terms from a.r to a.r^(n-1) are in both series and cancel out]

S.r - S = a.r^n - a

S.(r-1) = a.r^n - a

= a(r^n - 1)

So,

S = a.(r^n - 1) ÷ (r - 1)

In cases like Example 2, where r < 1, it is often written as:

S = a.(1 - r^n) ÷ (1 - r)

Geometric Progression Series Convergence

It is obvious that the numbers in the geometric progression series in Example 1 become larger and larger as n gets larger. The numbers in Example 2, however, get smaller and smaller, and the series sum tends to a finite number. This can be evaluated by making n = infinity, since for any number r < 1, r^n tends towards zero. The sum formula then becomes:

S = a.(1 - r^n) ÷ (1 - r)

= a(1 - 0) ÷ (1 - r)

= a ÷ (1 - r)

So for Example 2, the sum of the series to infinity is

S = 2÷ (1 - 0.5)

= 2 ÷ 0.5

= 4

Geometric Progression Series Summary

Geometric progression series are used throughout science and mathematics. The formula for the "n"th term, and the sum from the first term to the "n" term have been described and derived. They are often studied along with arithmetic progressions.

Geometic Progression Formula References

Each formula has been derived from first principles, although the article Sequences of numbers in generalized arithmetic and geometric progressions. describes both arithmetic and geometric progressions in greater detail.