The nth root of complex numbers
The modulus of the Pearcey Integral Function. Source: https://dlmf.nist.gov
In the previous post, we showed that any complex number to an integer power can be expressed as:
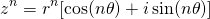
Where r is the modulus of that complex number, and θ is the angle between the complex number and the positive real axis. The question now arises on how we can compute the nth roots of a complex number. We'll start by considering the nth roots of unity.
The nth roots of unity
Definition: A complex number z is a nth root of 1 if it satisfies the equation
.
For smaller values of n, one can readily compute the numbers. For example, if n = 2, 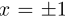 . If n = 3, we can factor the equation as a difference of cubes:
. If n = 3, we can factor the equation as a difference of cubes:
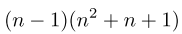
Obviously, x = 1 is a solution, but applying the quadratic formula to each of these yields 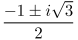 as well.
as well.
When n = 4, we can note that the solutions will be +1, -1, +i, and -i.
Now, let's try plotting each of these solution sets on the complex plane. We can see a pattern emerge:
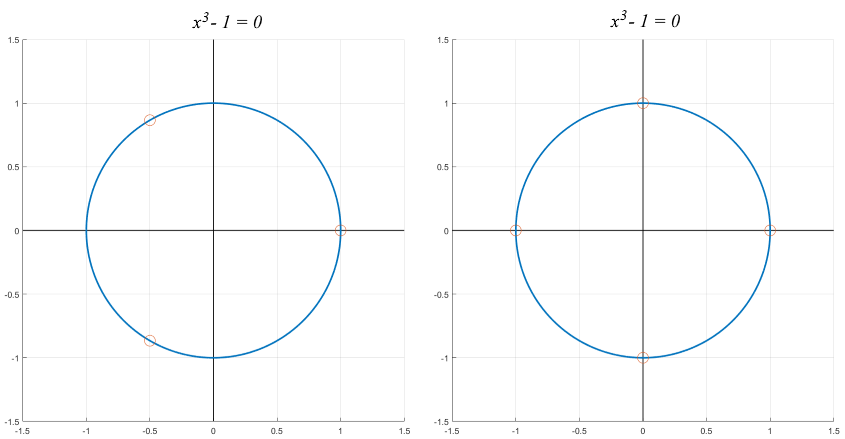
Original work. Images produced by in MATLAB
We can easily see that the zeroes of the function 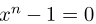 correspond to the vertices of a n-gon, centered at the origin, and inscribed in the unit circle. This also makes sense based on DeMoivre's theorem. The central angle of an n-gon contains 2π/n degrees. Adding the 2π/n to itself n times, gives us one full rotation of 2π radians, thus putting us back at the point 1 + 0i.
correspond to the vertices of a n-gon, centered at the origin, and inscribed in the unit circle. This also makes sense based on DeMoivre's theorem. The central angle of an n-gon contains 2π/n degrees. Adding the 2π/n to itself n times, gives us one full rotation of 2π radians, thus putting us back at the point 1 + 0i.
If the nth roots of unity are located at the vertices of a polygon, we can infer that the formula would be:
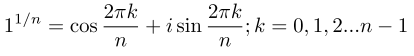
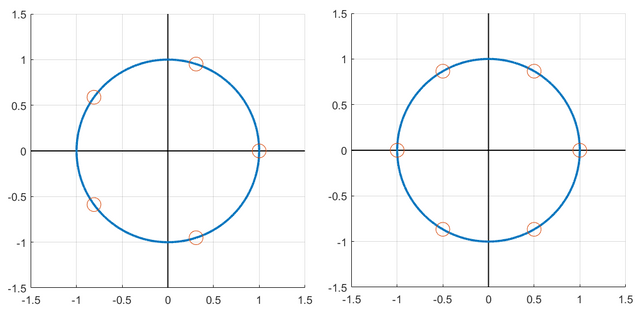
Continuing in this vein, we can plot all the fifth and six roots of unity:
And we can also compute them using the formula. For n = 5, we have: 1, 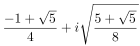 ,
, 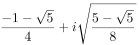 ,
, 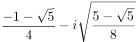 and
and 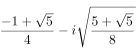 .
.
The sixth roots of 1 exist at multiples of π/3 along the unit circle; these are left as an exercise for the reader.
The roots of any complex number
The nth root of a complex number z is given by:
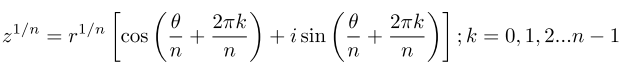
For example to calculate the 3rd roots of -1 + i, I would write:
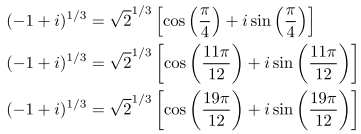
The last two expressions can be approximated by calculator if necessary. If I plot them on the complex plane, I get a diagram that looks like this:
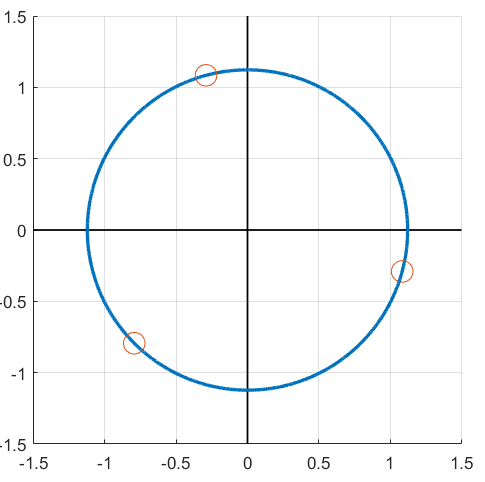
Note that this time the radius is slightly greater than 1, and that all of the points are slightly shifted away from the original position. However, all the points still form a regular polygon (in this case an equilateral triangle) centered about the origin.
We've now reached our goal of finding nth roots not just of 1, but of an complex number. I hope that this tutorial was insightful and as always if you have questions, don't hesiate to drop me a message below. I promise to do my best to answer them.
Very interesting post. I have upvoted you