Adding Numbers & Sigma (Sum) Notation

Hello. This post will be adding numbers with the sigma/sum notation. This particular math topic focuses on patterning, counting and adding numbers together.

This is a simplified version of my post on Sigma Notation from my website. This post focuses on finite sums and some basic sum formulas. No infinite sums nor sums with alternate signs are presented here.

Image Source

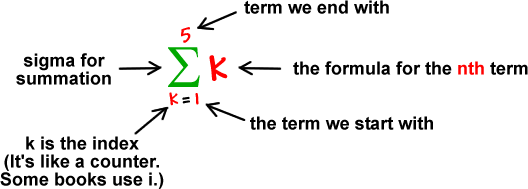
Finite Sums

---

The field of mathematics is full of numbers, symbols, ideas, theories and relations. A common theme in math is displaying ideas in a compact manner.

Instead of writing down 1 + 2 + 3 + 4 + 5 + ... + 10, we write the following instead:

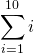
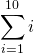
In the sigma (sum) notation we start from substituting i = 1 to get 1 as the first term. The next case is when i = 2 to get 2, then i = 3 to get 3 all the way to the upper limit of i = 10. Because there is an upper limit that is non-infinite in the sum, we have a finite sum. (A sum that never ends is an infinite sum which is not covered here.)

Image Source

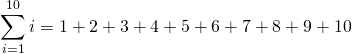
Another version of a finite sum is where the upper limit is an arbitrary positive integer. As an example we can have:

Image Source

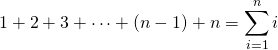
The variable n is a positive whole number. It could be 10, 15, 20, 1000, 74 or 500.

Extension

Sums do not necessarily have to start at i = 1. They could start at i = 3 and end at 8. Also, the variable i is an index variable and can be changed. (This is similar to for loops in programming.) Other index variable choices include the letters k and j.

Image Source

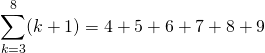
Sum Formulas

---

This section will briefly look at sum formulas. A more extensive look at sum formulas can be found in a university level Calculus course which focuses on Sequences and Series.

Here are a few sum formulas. (These start at a starting index of 1.)

Image Source

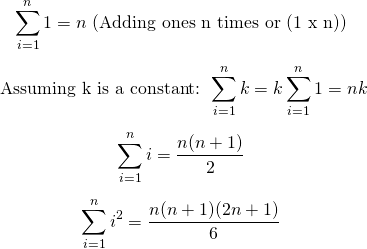
Examples

---

Example One

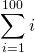
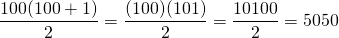
The sum 1 + 2 + 3 + 4 + ... + 100 can be represented by . Using the third formula from the previous section, this sum is equal to

Image Source

Example Two

Image Source

Example Three (Representing Fractions In A Sum)

There are cases where we add fractions. Consider this example.

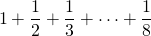
From term to term, the denominator increases by one. The sum above can be represented as:

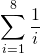
Practice Problems

---

Here are some practice problems. Please refer to the summation properties and formulas.

1. Find the sum of the numbers from 1 to 20 (including 1 and 20).

2. Find the sum of the numbers from 1 to 300 (including 1 and 300).

3. Evaluate the sum 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81 + 100 + ... + 225 using summation notation and/or formulas.

4. Find the sum of the even numbers from 1 to 40. That is, what is the total of 2 + 4 + 6 + 8 + ... + 40?

Solutions

---

Here are the solutions to the above problems.

Image Source

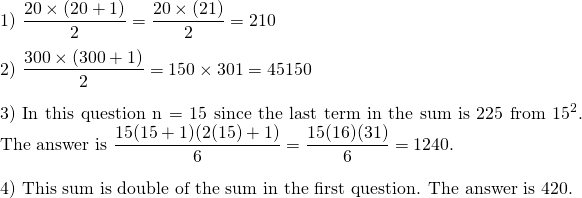
Notes

---

There are more topics related to sigma/sum notation, series and other types of sums which are not covered here. These include Taylor series, Maclaurin series, Riemann sums, index shifting on sums and alternating series.