[math, computation] properties of structure constant of SU(N)
[Sophus Lie-Wikipedia]
Today I am going to talk about some properties of structure constant of SU(N) group. I am a big fan of computing and deriving some mathematical stuff. But unfortunately, there are some technical issue of writing equations and expressing terms in Steemit. In this post I convert each equation into JPEG and upload it.
In the last post I mention Wilhelm_Killing [which was on Korean] and give some examples of computing killing vectors on two dimensional sphere. Since he is one of the pioneer of Lie algebras, I came up with Lie groups and its relevant exercise.
In group theory, typically in Lie groups, we frequently encounter the group generators and structure constants. Here focusing on SU(N), i'd like to show some explicit computation related with totally anti-symmetric 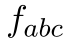 and totally symmetric
and totally symmetric 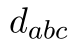 constants. Since I am considering on SU(N) group, the generators
constants. Since I am considering on SU(N) group, the generators 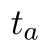 are traceless and hermitian.
are traceless and hermitian.
The generator satisfies
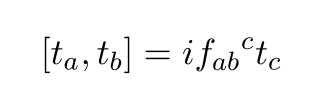
where 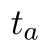 stands for generator and
stands for generator and 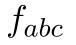 is structure constant.
is structure constant.
From Jacobi identity, we have
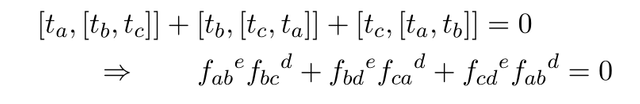
This is very important relation in many computation in Lie algebra.
Note In the semi-simple Lie algebra over complex number, we have a non-degenerate Cartan Killing form, (i.e. non-singular metric) which we can raise or lower the indices. Our SU(N) case belongs to this thus we have
Now I'd like to talk about representation. We can choose particular representation which decide some relation between generators, for example
where 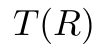
is called Dynkin index and 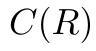 is called Casmir and R denote representation. We can pick particular values of Dynkin and Casimir by choosing particular group representation.
is called Casmir and R denote representation. We can pick particular values of Dynkin and Casimir by choosing particular group representation.
Here we will focus on the Fundamental representation. By imposing anti-commutation relation between generators we have some additional constant 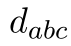
which is given by
Since in fundamental representation we have 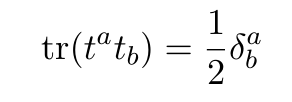
By contraction with generator and taking trace we can express explicit form of 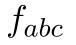 and
and 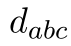
The detail procedure are given as follows
Note in the process we used traceless property of generators of SU(N)
At this moment, we can talk about symmetric properties of these constants which is the purpose of this post. It is well known that 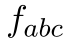 is totally anti-symmetric and
is totally anti-symmetric and 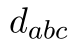 is totally symmetric. At my first trial of exercise of showing this in SU(3) i show this by explicit computation using Gell-Mann matrices, and find all non-vanishing constants. One of my friend ask is there any other ways of showing this properties, not by exhausting computation? and at that time i didn't know this method. After some familiar with these topics i noticed this method, and i think it is good time to share this method.
is totally symmetric. At my first trial of exercise of showing this in SU(3) i show this by explicit computation using Gell-Mann matrices, and find all non-vanishing constants. One of my friend ask is there any other ways of showing this properties, not by exhausting computation? and at that time i didn't know this method. After some familiar with these topics i noticed this method, and i think it is good time to share this method.
Since these constants are written in terms of trace, i guess one of you already get answer. Using the property of trace 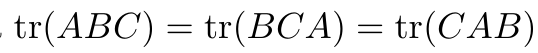
we can show it more convenient way. The detail process are given as
Now we can see indeed 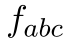 is totally anti-symmetric and
is totally anti-symmetric and 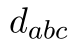 is totally symmetric!
is totally symmetric!

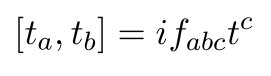
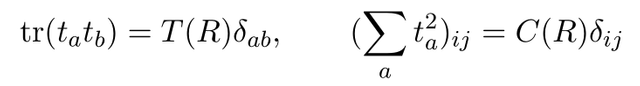

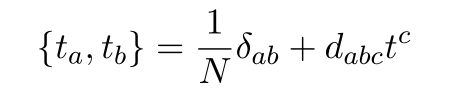
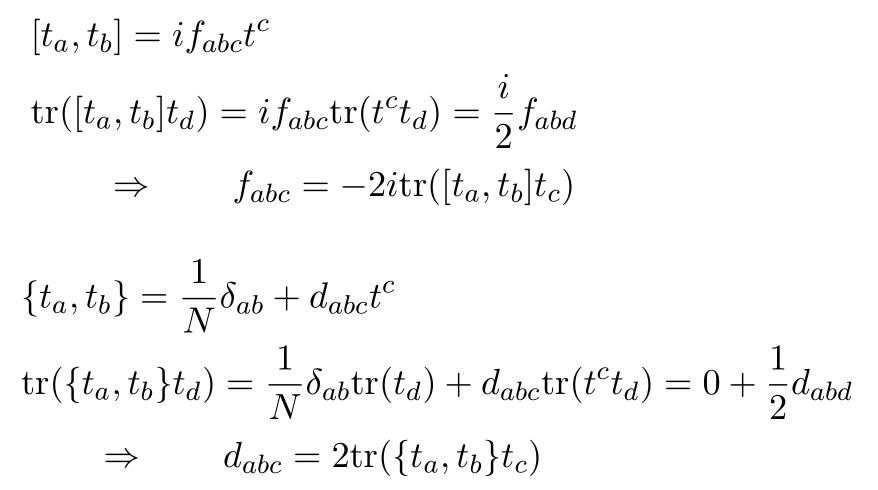
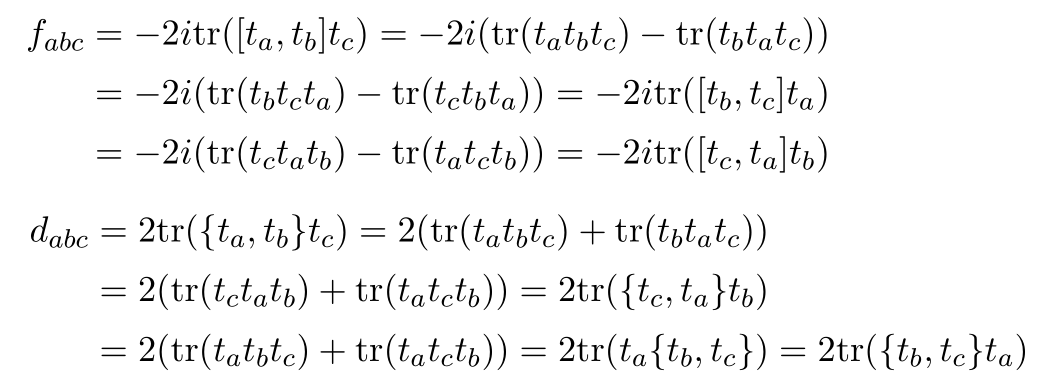
I feel you may want to define Lie groups first, or at least give a moviations for Lie algebras. And it's also notable that you use (anti-)commutators without introducing them first. This way, this will have a very narrow range of people who can understand it, while not knowing it already. Maybe add more links in the intro too - although of course that's work.
PS In English, I (i.e. "me") is written with a capital I and it's "i.e." and not "i.e,".
Keep up the good work
@qed
@qed, Nice comment and thanks for your attention. The reason why I did not define Lie group and for other motivation or explanation for some notation is in some sense i'd like to make some other post to explain them in more detail. If I include every details of basic things into a one post, I think that both novice and some relevant student may lose their attention on this post. So at that purpose, I write this post aiming some relevant student who study this subject. In some days, I will try to make a post for general audience. Anyway I understand your meaning and try to adapt your opinion in my future posts.
And thanks for clarifying my English and attention to my post. I will apply your words
Thanks, look forward to more posts.
!-=o0o=-!
To follow curated math content follow @math-trail.
If you wish @math-trail to follow you then read this article.
Click here for Mathematics forum on chainBB
Cool.
Take care!
Btw. there is a Wiki by a frantic guy who classifies groups in unending detail
https://groupprops.subwiki.org/wiki/Main_Page