When Math and Art Collide
In 2012, an interdisciplinary group composed of French mathematicians and computer scientists gave the math world (which includes the real one) a new, beautiful object: the isometric embedding of the square flat torus. If you're wondering what I just said, it is the 3-D rendering of a inescapable square. Their creation blurs the lines of art and math: it is both mathematically and aesthetically pleasing. It is also one example of a smooth fractal: a fractal that looks smooth when zoomed out, but appears corrugated and rough when zoomed into.
To begin understanding the uncanny beauty of this far-fetched object, we need to understand what a flat square torus is.
A flat square torus is a square whose sides are pairwise identified, meaning that the sides opposite to each other are linked. If I were to have an object on the torus move from left to right, crossing the edge of the right side of the square, it would reappear out of the left side of the square. The same occurs with the up-down sides.
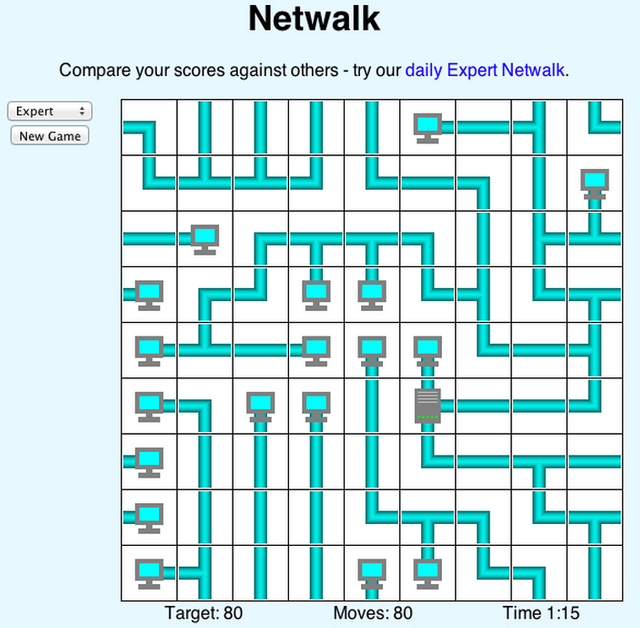
Many computer games, such as Netwalk, use a similar concept:
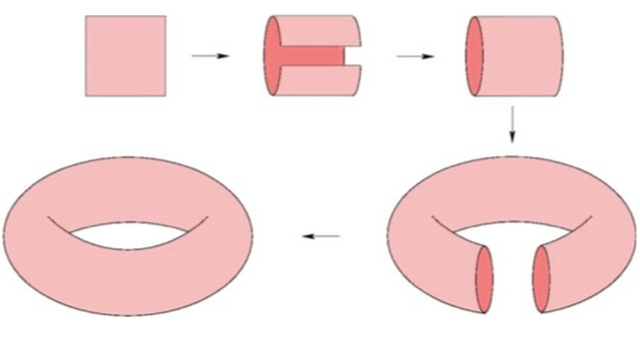
But what if we wanted to make this a 3-dimensional object? After all, it is quite simple to embed (fancy term meaning to make a 2-D object 3 dimensional) a normal square in 3 dimensions by stretching out their face to make a cube with the exact same face dimensions that still obeys the characteristics of the original square. To embed a flat square torus with the same characteristics, we must fold the sides and attach them to each other to create a cylinder. Then, the cylinder must be stretched into a hollow ring.
The issue with this embedding is that this new object does not respect the actual dimensions of the original flat square torus. It seemed that there was no 3-D model of the flat square torus, that all representations of it would break the dimensions of the original shape. This remained the case for a very long time, until mathematicians N. Kuiper and Nobel Prize Winner J.Nash proved the existence of a solution to this issue.
Nash's big breakthrough was that this problem could be surmounted, if a bent torus had an infinite amount of points on which acceleration cannot be defined. But what does that mean?
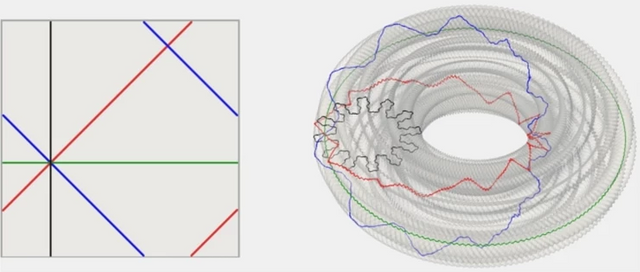
Let's take a look at the above picture. In Class C0, there is a huge change of the slope at the green point, so much so that the slope cannot be defined at that point. In Class C2, the slope is so smooth that there is so little discontinuity (change) that a skater riding it would not feel a thing change. In Class C1, however, at the green point, the skater would suddenly feel a force acting on him. Nash proved that this case must happen an indefinite amount of times on the torus.
Unfortunately, in mathematics, proving the existence of something and showing it are two very distinct things. The thief allegory explains this relation best: let us assume that some people are in a closed room with a jewel. Suddenly the lights go off, and flicker back on, revealing that the jewel is missing. This proves the existence of a thief among the people in the room, but does not reveal who it was. Nash had no physical model to show his solution.
This is where fractals, and non-differential curves (curves which are continuous but do not radically change their slope), come in.
For those of you that do not know what a fractal is, it is an infinitely repeating pattern caused by the application of a mathematical equation. In nature, they are non-differential curves.The most famous example is the Mandelbrot Set:
Beautiful, aren't they?
It is conceivable then, to imagine that the solution to our problem would be a fractal. All you would need is to get a length for the square and fold the sides infinitely. However, to create an accurate model, we need something with Class C2 attributes, which is something that fractals do not posses (their edges are too rough).
The research team at Hévéa (a French research firm) created a rendering using algorithms that had both the smoothness of classical objects and the roughness of fractals. What they got was a smooth fractal.
One of the interesting properties of a smooth fractal is that the closer you get to it, the rougher it looks. The farther away you are, the smoother it looks.
The team discovered to their amazement that their model still obeyed the dimensions of the original square they used.
What is even more mind-boggling is the fact that the lines on each object are all the SAME LENGTH.
The conclusion brought about by this discovery is both strange and startling: given enough edges, any object can be isometrically replicated. Shrink a basketball to a microscopic size, add corrugations (not folds), and the final product will have the same dimensions as the regular basketball. This beautiful masterpiece, very pleasing to the eye, is literally made possible by math. Crazy, right?




Peace @augmdc
Thank you for posting your informative publication on steem blockchain.
I would like to welcome you on steem and share this information with you.
Do you know that partiko is a steem mobile application that can help you earn fairly steem power ? If you want to increase your potential to blog on steem ecosystem feel free to ask on my latest post.
Warm regards.
Posted using Partiko Android