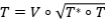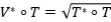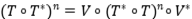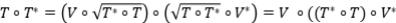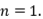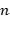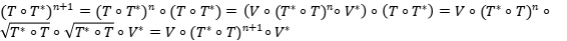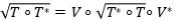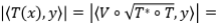EJERCICIO DE OPERADORES II (Proyecciones ortogonales)
PRELIMINARES
Sea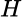 
un espacio de Hilbert y 
sus operadores acotados. Se dice que es un operador proyección, si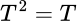 
. Es directo ver que para una proyección 
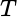se tiene que 
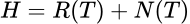. En caso de darse 
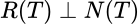, diremos que la proyección 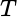es ortogonal. Dado un subespacio 
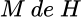, sabemos que 
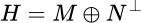. Es directo ver que
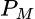, definido por 
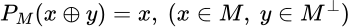es una proyección ortogonal y toda proyección ortogonal es de esta forma.
Un subespacio 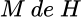, se dice que es invariante para un operador 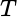, si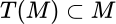 
. El operador 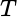, se dirá lleno, si para todo 
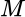subespacio invariante para 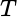, se cumple que 
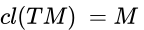(clausura en la topología de la norma). Un operador 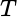, es lleno, si y sólo si, dado 
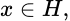con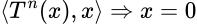 
. Un subespacio 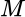se dice que reduce al operador 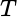, si tant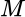o como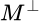 
son invariantes para 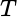. Por lat( 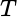) denotamos todos los subespacios invariantes para .
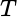Dado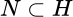 
, denotaremos a la clausura de la variedad lineal generada por 
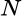mediante 
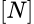. Para 
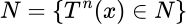escribiremos simplemente =
.
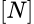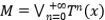Finalmente, recordemos que si 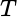es un operador, existe una isometría parcial 
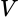tal que 
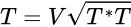. A este resultado se le conoce como el teorema de descomposición polar.
(2).
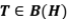
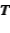
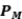
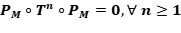
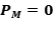
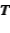
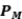
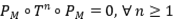
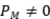
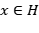
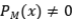
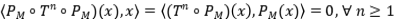
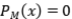
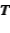
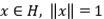
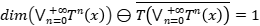
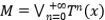
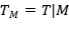
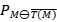
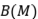
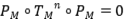
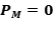
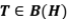
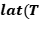
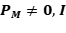
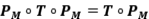
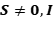
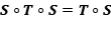
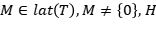
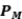
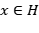
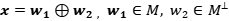
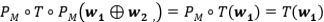
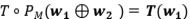
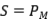
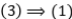
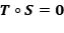
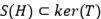
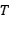
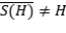
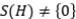
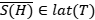
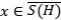
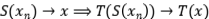
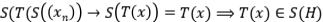
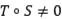
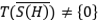
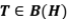
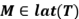
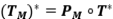
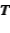
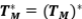
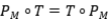
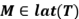
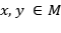
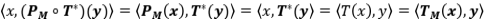
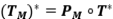
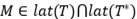
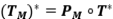
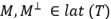
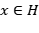
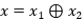
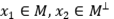
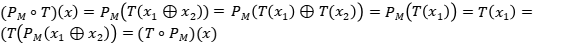
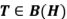
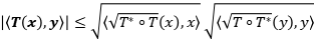
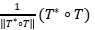
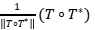
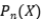
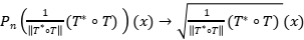
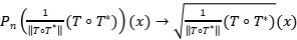
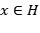
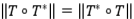
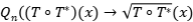
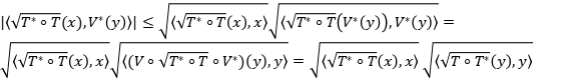
Ejercicio 13: Halle proyecciones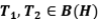 
tales que que 
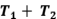no sea una proyección.
Solución: Considere lo operadores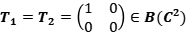 
. Es claro que son proyecciones y 
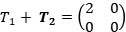no es una proyección.
Ejercicio 14: Sean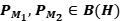 
proyecciones ortogonales, tales que 
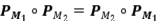. Probar que 
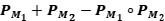es una proyección ortogonal sobre 
.
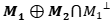Solución: Primero demostremos que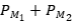 
es una proyección ortogonal, si y sólo si, 
.
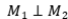Supongamos que 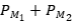es una proyección ortogonal. Demostraremos que 
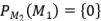. Como 
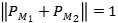, tenemos que para 
=
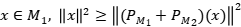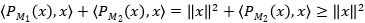. Se deduce que 
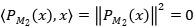y por lo tanto 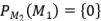. Es decir 
.
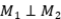Realmente, usando el argumento anterior, podemos demostrar que
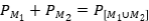
Para demostrar el resultado observe que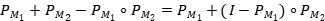 
. Tenemos que 
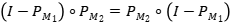es una proyección ortogonal de la forma 
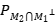y como 
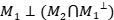se deduce el resultado.
Ejercicio 15: Sean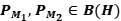 
proyecciones ortogonales. Pruebe que 
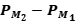es una proyección ortogonal, si y sólo si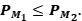 
Solución: Si es una proyección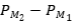 
, entonces 
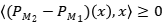, de lo que se deduce el directo.
Recíprocamente, si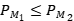 
, entonces 
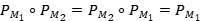.Tenemos por lo tanto que 
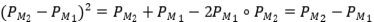y como 
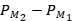es auto adjunto, se deduce el resultado.
Ejercicio 16: (1) Sean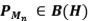 
proyecciones ortogonales, para cada n=1,2,3…; tales que 
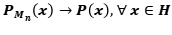en la topología de la norma. Probar que 
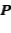es una proyección ortogonal. (2) Puede ocurrir que las 
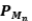proyecciones ortogonales sean de rango finito y 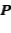de rango infinito; o cada 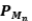de rango infinito y 
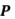de rango finito.
Solución: (1) Es claro que 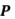es una aplicación lineal sobre 
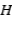. Veamos que realmente esa acotada. Si 
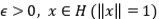, tenemos que
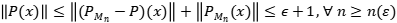. Se deduce el resultado.
Como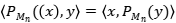 
→
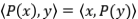, obtenemos que 
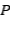es auto adjunto. Finalmente 
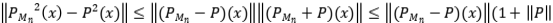. Se deduce que 
.
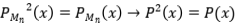(2) Considere para el primer caso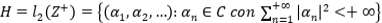 
.
Sean los operadores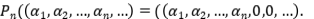 
. Es claro que cada 
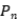es de rango finito y 
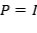el operador identidad. Para el segundo caso, sean 
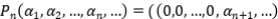. Cada es de rango infinito y 
.
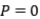Ejercicio 17: Sean 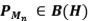proyecciones ortogonales, tales que 
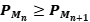para cada n=1,2,3…; probar que existe 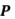una proyección ortogonal tal que 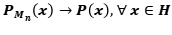en la topología de la norma. Describir el rango y el núcleo de .
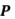Solución: Supongamos que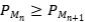 
. Tenemos que 
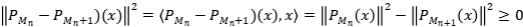. Como la sucesión
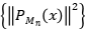es acotada y monótona, converge; por lo tanto 
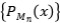es de Cauchy y convergente a 
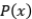. Ya hemos visto que 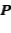es una proyección ortogonal. Por otro lado como 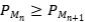, deducimos que 
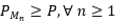. Por lo tanto 
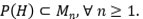. Es decir 
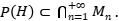. Si 
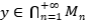, entonces 
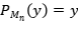. Pasando al límite deducimos que 
.
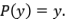Estudiemos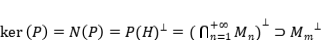 
. Por lo tanto 
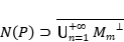. Por otro lado 
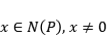. si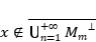 
, entonces 
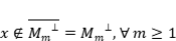. Es decir 
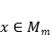, luego 
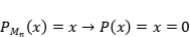, lo que es contradictorio.
Ejercicio 18: Sean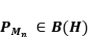 
proyecciones ortogonales, tales que 
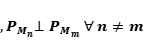. Probar que 
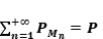es una proyección ortogonal.
Solución: Como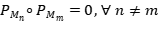 
, dice que 
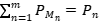es una proyección ortogonal. Tenemos que 
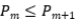y además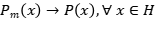 
en la topología de la norma. Se deduce lo afirmado.
FUENTE
Erwin Kreyszig (1978): Introductory Functional Analysis with Applications. John Willey & Sons. New York.