Hello its me again. Today we continue our talk with Logical (Boolean) Functions. I will talk about different ways of representing a Logical Circuit using Boolean Expressions-Functions and Truth Tables (Circuits/Gates will come some posts later!). I will also show you how to get an Boolean Function from an Truth Table using Minterms and Maxterms (next 2 posts we will talk about simplifing this function). So, without further do. Let's get started!

Boolean Functions/Expressions:

    Boolean Functions/Expressions are used for Logical Circuits. We use an Mathematical Representation of the Inputs and Outputs of an Logical Circuit to get Output values for each different value of Input, without the need of testing it on real hardware. It is much easier to have a function that we can afterwards translate into an Circuit then creating a Circuit directly, cause we would have to test each value by ourself.

    The values that such an function can get are binary numbers. So, we can only have 0 or 1, cause an Circuit can only have low and high voltage readings, as we already said last time. So, we will write an Mathematical Expression that contains those Inputs and does Boolean Algebra (next post) to them, to get an specific Output.

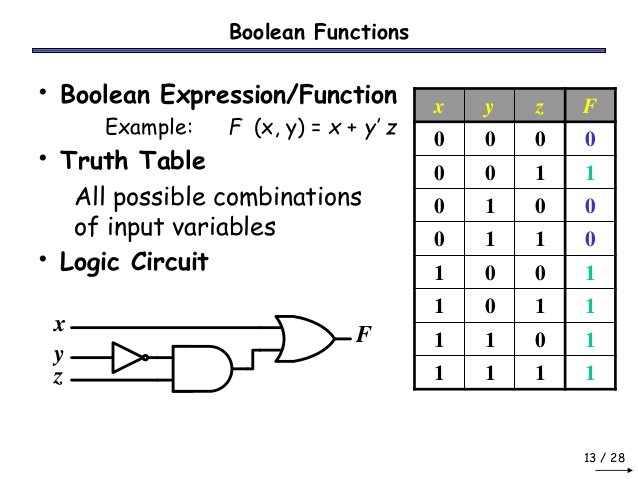
So, an Boolean Function looks like this:

F(x, y, ...) = x + y' + xy ...

where x, y, ... are the Variables/Inputs and F is the output that comes when putting those Inputs into the Boolean Function F

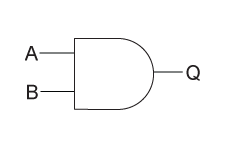
For example an AND Gate (we will talk about all Basic Gates later on)

can be represented as a Boolean Function like that:

Q(A, B) = AB

Things that apply to an Boolean Function are:

• each element of a function is either a sum or an product, sums are called maxterms and products are called minterms
• the function can be described as an sum of products or an product of sums
• a function needs to be in conjunctive normal form, where each variable appears only 1 time (to convert into this form we use simplification)

Truth Tables:

    In the same way as we use Logical/Boolean Functions, we also use Truth Tables. An Truth Table contains all different kinds of Inputs and the Outputs an Circuit gives. We can go from a Truth Table to a Boolean Function using the easy Minterm and Maxterm way,  Karnaugh Maps and the Quine McCluskey Method (the first one comes some posts later, the second one much later on), and the opposite can by done easily simply putting the Input values into the Function and writing the Output in the Truth Table or testing all Inputs directly on an Circuit that implements the Function.

    As you can imagine already:

• an Truth Table can get really big, when having many Inputs inside of our Circuit. 
• an Logical Circuit can have only 1 Truth Table, but more Logical/Boolean Functions that describes it (we will find the most simplest one)
• each row of the Truth Table represents an minterm or maxterm

For example if we have 3 Variables X, Y, Z and the values of them are 0, 1, 1, we can represent this row as:

x'yz (minterm) or x+y'+z'(maxterm)

So, some pretty easy rules that apply are:

Minterms:

• Variables with 0 get a '
• Variables with 1 get nothing
• Product of those Variables

MaxTerms:

• Variables with 0 get nothing
• Variables with 1 get a '
• Sum of those Variables

Writing the Boolean Function using the Truth Table:

    An easy way of getting the Circuit Boolean Function from an Truth Table is using the Minterms and Maxterms we talked about. We will insert/insert not depending on the Output Value and the "way" (minterm or maxterm) we use for doing it.

Using Minterms:

We write down a sum of minterms, having the row's output where the minterm appears have a value of 1. 

So, the Truth Table I had before has an Boolean Function that looks like this:

F(x, y, z) = x'yz + xyz

Using Maxterms:

We write down a product of maxterms, having the row's output where the maxterms appears have a value of 0.

So, the Boolean Function now looks like this:

F(x, y, z) = (x+y+z)*(x+y+z')*(x+y'+z)*(x'+y+z)*(x'+y+z')*(x'+y'+z) (much bigger yeah)

    We will use the "way' that gives us less elements in our Function, so when having less 0's we will use Maxterms and when having less 1's we will use Minterms. The way a function looks like using Minterms makes it easier to read, so we will try to use Minterms for most stuff!

This is the end of today's post! Hope you enjoyed it!

    Next time we will get into Boolean Algebra and Simplification Theorems that apply to Boolean Functions. That way we will learn to simplify Functions using the way I showed you today, applying those newly learned Theorems that will  make our boolean function smaller, so that we then create simple logical circuits! And the post next to that, will be about the Karnaugh Map way of getting an already simplified function!

See ya soon...Bye!