Logic Design - From Function to Circuit using Multi-Input Gates
It's a me drifter1 again! Today we will talk about Multi-Input Gates and how we get a Locigal Circuit using an Booleal/Logical Function! I will first start off with Multi-Input Gates and then we will get into the Function to Circuit stuff. So, let's get started!
Multi-Input Gates
In the last 2 Logic Design Posts I started talking about 2-Input Basic and Universal Gates. And yes, we can create any Circuit using only those and the Circuits I'm gonna show you basically again use the Basic ones to be created! But, to make a Circuit even more simpler and smaller we can use 3, 4, 5-Input Gates that instead of many following Basic Gates!
Example:
Suppose we have an Function that looks like this: F(A, B, C) = A + B + C. This function can be represented by an OR-3 Gate, cause we use the OR Operation on 3 Variables!
We can use Boolean Algebra and turn it into this: F(A, B, C) = (A + B) + C. This time we have 2 Simple OR Gates, where the second one has as Input the Output of another one (that has A and B as Input) and Input C.
So, you can already see that instead of using 2 OR Gates we can use 1 OR-3 Gate and minimize our Gates! That's exactly the reason why I make this post today!
Let's start out with how the Gates we talked about (Basic and Universal) change when they have more then 2 Inputs. And never ever say that an NOT Gate can be Multi-Input, cause it has 1 Input and 1 Input and simply acts as an Inverter of 0 -> 1 and of 1 -> 0!
OR Gate:
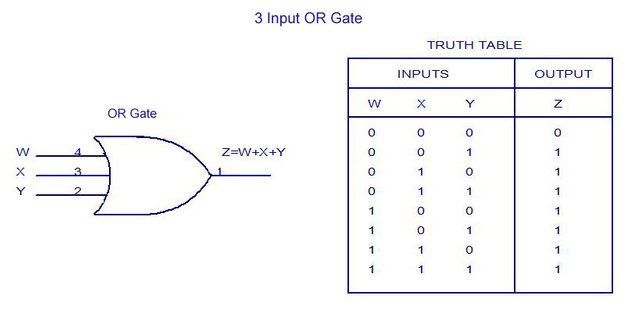
An Multi-Input OR Gate, works the same way as the 2-Input one! When either of it's N inputs has a value of 1, the Output will be 1. So, it has an Output of 0 only when all Inputs are 0!
The Truth Table explains exactly what I meant. The Symbol also doesn't change, but it has only more Inputs. You can continue on using OR-4, OR-5, OR-6 Gates etc.
AND Gate:
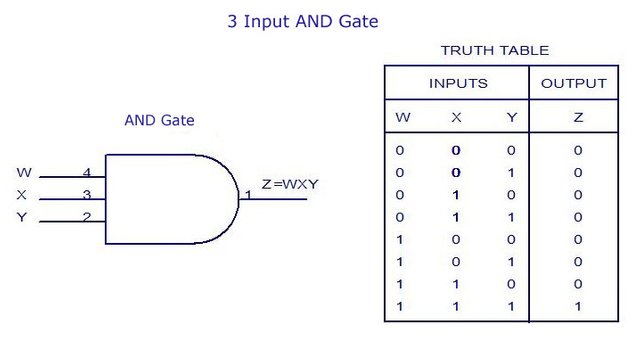
An Multi-AND Gate again works like an normal AND Gate. It has an Output of 1 only when all Inputs have a value of 1!
The Truth Table again explains what I said and you can also see that we use the same Symbol. You can again use AND-4, AND-5 Gates etc.
XOR Gate:
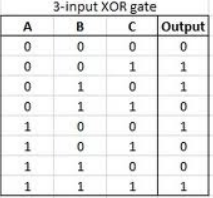
The XOR Gate is another story. This time the Logic actually changes! In normal XOR Gates we said the the Output is 1 when the Inputs differ, but this time we say that the Output is 1 only when the number of Inputs with value of 1 is odd (1, 3, 5 etc). So, we will have an Output of 0 when the number of 1's is even!
If you look at the Truth Table you will see that the Outputs are 1 only when we have odd 1's as Input. The Symbol is also the same, but I don't found a good picture online :D You can again expand into XOR-4, XOR-5 Gates etc. using the concept of odd I told you!
XNOR Gate:
The exact opposite of an XOR Gate is and XNOR Gate. It has the opposite Truth Table and you can think exactly like that about it. So, we have an Output of 0 when number of 1's in Input is odd or to say it better the Output is 1 when the number of Inputs with value 1 is even! And we have an Output of 0 when it is odd.
Again, you can see that the Truth Table does what I said. Only when number of 1's is even we have Output of 1! I couldn't find a Symbol that was good again, but the Symbol is the same with more Outputs and we can again expand into XNOR-4, XNOR-5 Gates etc. using the Concept of even!
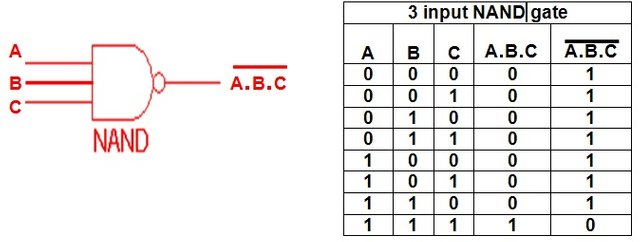
NAND Gate:
A NAND Gate is the opposite of an AND Gate! So, even when having more Inputs we will have an Output of 0 when all Inputs are 1 and an Output of 1 in any other case!
The Truth Table does exactly what I told you and the Symbol is again the same but with more Inputs! You can expand into NAND-4, NAND-5 Gates etc. having the Output be 0 only in the last row where all Inputs are 1!
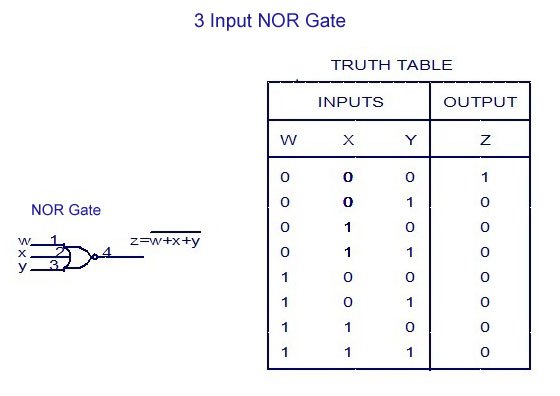
NOR Gate:
An NOR Gate is the opposite of an OR Gate. An OR Gate has 0 only when all Inputs are 0, so an NOR Gate has Output 1 only when all Inputs are 0! So, in each other Case we have an Output of 0.
The Truth Table again looks as I described! The Symbol is the same but with more Inputs and you can again expand into NOR-4, NOR-5 Gates etc. having only the first row where all Inputs are 0 have an Output of 1 and the rest 0!
So, after the Introduction into Multi-Input Gates let's now get into how we translate a Function into a Circuit!
From Function to Circuit:
I will talk about how we identify each and every of the Basic and Universal Gates in our Function! And using Boolean Algebra you can then maybe even change some parts in our Function to make it even better and smaller, containing less Gates! Remember less is more :)
NOT:
A NOT Gate is pretty easy. Every time you see a Variable alone have an NOT Symbol on it ' or _ you know that we have to invert the Variable's Input and use a NOT Gate!
So, A' is Input A followed by a NOT Gate.
OR:
A OR Gate is also pretty simple. The OR Symbol is + and all the elements that are in this sum will be Inputs of an OR Gate. So, an Sum of Minterms translates into an OR Gate, if you like thinking about it that way.
So for F(A, B, C) = ABC + (A+B)' + A⊕C, we will have an Output that comes from an OR-3 Gate, cause we have 3 Elements in our sum! The Inputs of this OR-3 Gate will be the Outputs of ABC, (A+B)' and A⊕C and this Elements can be anything we wish!
AND:
An AND Gate is also pretty simple. The AND Symbol is nothing or * and all the elements inside of this product will be Inputs of an AND Gate. This product of Maxterms translates into an AND Gate.
So for F(A, B, C) = (A+B+C)(AB)'(A⊕C)', we will have an Output that comes from an AND-3 Gate, cause we have 3 Elements in our product! The Inputs of this AND-3 Gate are the Outputs of A+B+C, (AB)' and (A⊕C)' and we can again have them be anything. (I don't know if you saw what I did, by I actually used a similar Function to the OR's one, but it's not the same, because I don't used the De Morgan Law!)
XOR:
A XOR Gate is also pretty simple. You just have to search for the XOR Symbol ⊕, but this is the easy way. Sometimes a XOR is not visible and we can create one by finding the following inside of our function:
A⊕B = A'B+AB' (pretty easy one)
A⊕B⊕C = AB'C' + A'BC' + A'B'C + ABC (in the first 3 Elements 1 Variable is not inverted each time and in the last all are not inverted)
I think you don't need more than that...
XNOR:
A XNOR Gate can be found by searching for (A⊕B)' or AXNORB directly that is rare. But, we can again search for the following inside of our function:
(A⊕B)' = AB + A'B' (pretty easy one)
(A⊕B⊕C)' = A'B'C' + ABC' + AB'C + A'BC (in the first Element all Variables are inverted and in each of the other 3, one Variable is Inverted every time)
NAND:
A NAND Gate is the opposite of an AND Gate and we can find it diretly like that: (ABC...Z)'. You can also find it in the De Morgan Law form that is (ABC...Z)' = A' + B' + C' + ... + Z'. So, when having many NOT's in a sum, we can make it into an product that get's inverted and so we come up with an NAND Gate!
NOR:
A NOR Gate is the opposite of an OR Gate and you could find it that way directly like that: (A+B+C+...Z)'. But, sometimes you will find it n the De Morgan Law form that is (A+B+C+...Z)' = A'B'C'...Z'. So, when having many NOT's in a product, we can make it into a sum that get's inverted and get a NOR Gate!
This was actually it! So, finally let's get into an example!
Example:
From an given Function we will create an Circuit checking if we found any of the things I talked about! This Circuit will contain only Gates and not more advanced Circuits in which we get from next time!
The Function is the following:
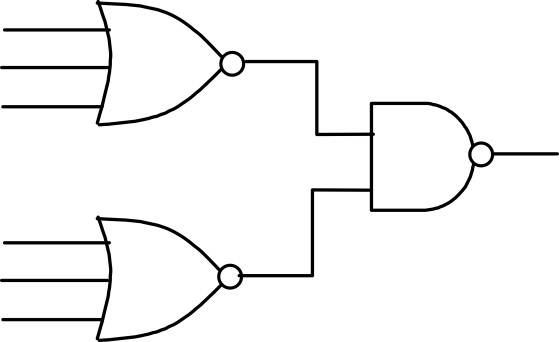
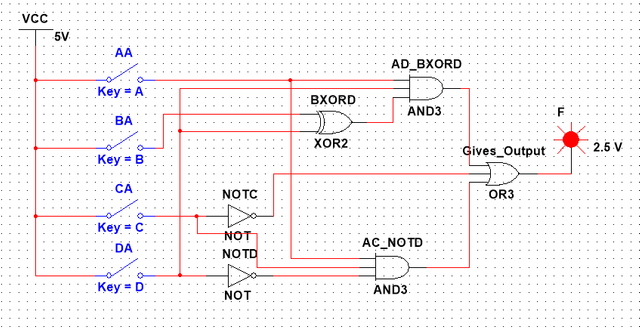
F(A, B, C, D) = AD(B'D + BD') + C' + ACD'
- We have 3 Elements in our Sum, so the Output will come from an OR-3 Gate
- The 2nd Element is an Input passed through an NOT Gate
- The 3rd Element is an AND-3 Gate, cause it contains 3 Elements in a product. The last Input of this Gate will be inverted (D')
- The 1st Element is an AND-3 Gate, cause it contains again 3 Elements in a product. The last Input this time is the Output of another Gate that is representing an XOR Gate (B'D + BD' = B⊕D).
So, we end up with this Circuit in Multisim(we will get into that later on):
This is the end of todays' post! Hope you enjoyed it!
From next time on we will get into more Advanced Circuits that we use like Gates in our Logical Circuits. We will start out with Adders tomorrow!
Bye!