A Simplified Glimpse into Quantum Mechanics: Bell’s Theorem

Hi everyone!

Recently, I’ve read about Bell’s theorem, named after the CERN physicist John Stewart Bell, and I believe it must really be the starting point if one wants to understand why quantum mechanics is truly magical, in a shockingly simple way. I will also be explaining some of the fundamental principles of quantum mechanics along the way - stay tuned!

LHC at CERN

Bell's theorem simply states that:

“No physical theory of local hidden variables can ever reproduce all of the predictions of quantum mechanics.” (1)

where “theory of … hidden variables” refers to any theory arguing that quantum particles seem to behave randomly just because we don’t know about all of the variables governing their behaviors. They’re actually deterministic and there’s nothing super surprising about them. One can predict their behaviors exactly, once all hidden variables are known to the experimenter.

Additionally, in the simple statement of Bell's theorem, “local” refers to Einstein’s principle of “local realism”, which is the combination locality and realism, explained below:

• The principle of locality states that any physical object can only have an impact on another in its immediate surroundings, or similarly, the speed of no cause-and-effect relationship can exceed the speed of light in vacuum.
• The principle of realism can be best explained by Einstein’s famous statement: “I like to think that the moon is there even if I’m not looking at it.” So, simply, realism argues that a certain property, e.g. position, of a quantum particle has a real value, even before any measurement takes place.

This principle of realism has its roots in a paper published by Albert Einstein, Boris Podolsky and Nathan Rosen, now famously known as the “EPR”. EPR paper presents a proof that basically says: EITHER there are hidden variables governing quantum particles and that’s why it seems like they behave randomly, OR Heisenberg Uncertainty Principle is true, and quantum particles are indeterministic.

Heisenberg Uncertainty Principle says that there is always a certain degree of uncertainty associated with the values of particle properties, e.g. velocity, position or energy. The values of these properties are not real or defined until the particle is observed. That is to say that, for example, it doesn't make any physical sense to talk about the position or velocity of an electron before any measurement takes place, which is incredibly counter-intuitive considering our view of reality in daily life.

Now, let us reformulate Bell’s theorem in the light of these explanations:

If you are convinced that no object can influence another object in its surroundings faster than the speed of light in vacuum and that the moon is there even when you're not looking, and you create a theory claiming that the behavior of the electrons is actually deterministic, (contrary to the modern interpretation of quantum mechanics) basing this argument on the existence of a hidden variable yet unknown to us, your theory cannot reproduce the accurate predictions of quantum mechanics, according to the mathematical theory of probability.

Now, to convince you all of the correctness of the statement above, let’s look at a shockingly simple proof of Bell’s theorem, which describes the possible results of the following experiment assuming any local hidden variable theory is true:

Let’s say that we have a photon, a particle of light and we’re interested in measuring its “polarization angle”, that is, whether the particle oscillates at a specific angle, by exposing it to different polarizers and seeing whether any of its components makes it through the polarizer.

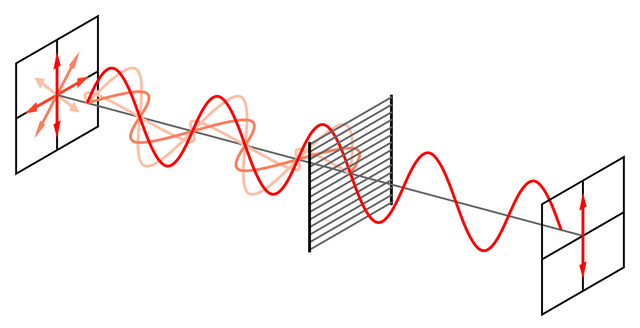
As an example, please take a look at the picture above. A photon can oscillate at many different angles, and to find out whether it oscillates at 90 degrees we can just let it pass through a polarizer like the one in the middle in the picture above. Now, since there is a component of the photon getting through this polarizer, we say that it oscillates at 90 degrees. Similarly, this remaining component of the photon oscillating at 90 degrees understandably can't make it through a second polarizer angled at a different angle than 90 degrees, because the remaining component doesn’t oscillate at an angle other than 90 degrees.

Now, let’s assume that we have a photon with a definite oscillation (i.e. oscillation exists or not) at 3 different angles - 0, 120 and 240 degrees - and define the following questions to answer them by conducting the corresponding experiment:

• X: Does the photon pass through a polarizer angled at 0 degrees?
• Y: Does the photon pass through a polarizer angled at 120 degrees?
• Z: Does the photon pass through a polarizer angled at 240 degrees?
• XY: Is the answer to X and Y the same? That is, would the photon make it through two polarizers, one of them angled at 0 degrees, and the other at 120 degrees?
• YZ: Is the answer to Y and Z the same? Similarly.
• XZ: Is the answer to X and Z the same? Similarly.

Since we are designing the experiment assuming any local hidden variable theory, we also assume that, according to the principle of realism, a yes-or-no answer to the question “Does the photon pass through a polarizer set at an angle of A degrees?” exists before we even make any measurements, opposing the Heisenberg Uncertainty Principle of quantum mechanics, according to which this answer doesn't exist.

Now, let's describe all possible outcomes of the experiments answering the questions above with the table below:

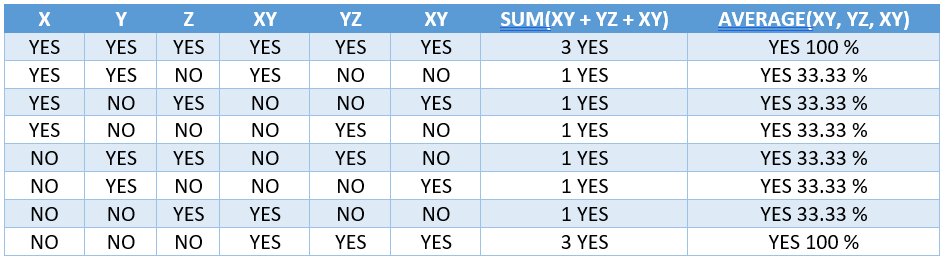
This table shows that, assuming any local hidden variable theory, if we repeat the experiments XY, YZ and XY and sample the results in a uniformly random way from one of the experiments, that is, in a way that we don’t prefer sampling the yes-or-no answer from any of these three different experiments, we will get a YES answer from AT LEAST 33.33 % of the samples.

However, quantum mechanics predicts that you would actually get a YES answer from 25 % of the samples, which does not comply with the predictions of any local hidden variable theory. This is Bell’s inequality, based on a simple probability experiment.

So, this leads us to the following:

There is no universe in which both quantum mechanics and any local hidden variable theory could be right.

Considering the fact that quantum mechanics is one of the most successful theories in terms of its predicting accuracy of the experimental results, which sometimes even exceeds nine digits after the decimal point, and that the probability theory is a well-established branch of mathematics, anyone still willing to accept a hidden variable theory must also submit to non-locality. This submission would be either in the form of accepting that there are interactions faster than the speed of light in vacuum, which clashes with the theory of relativity OR or that the universe is governed by superdeterminism, which is to say that the future is already determined to happen in a certain way and there is no free will.

Therefore, Bell's theorem effectively leaves anyone who argues that there is nothing magical about the behaviors of quantum particles,with an almost religious choice: take a stance against the theory of relativity OR deny free will.

If we consider how simple the proof was, this is absolutely insane.

Thus, according to our best scientific and mathematical theories, we are living in a truly unreal universe where we are made of particles whose positions, velocities or energies do not really have a real value before any observation takes place.

Next time you're not looking at the moon, don't be so sure that it's still there ;)

(Caution: The previous sentence was just a literary device!)

1 - C.B. Parker (1994). McGraw-Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. p. 542. ISBN 0-07-051400-3. Bell himself wrote: "If [a hidden variable theory] is local it will not agree with quantum mechanics, and if it agrees with quantum mechanics it will not be local. This is what the theorem says." John Bell, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press, 1987, p. 65.

Acknowledgements:
I was inspired by the mathematical example in the article by David R. Schneider to develop my example above described as a proof of Bell's inequality: http://drchinese.com/David/Bell_Theorem_Easy_Math.htm

Thank you very much for reading my post, and please feel free to follow me & resteem the post so that I can reach a larger part of the community with it! :)