[선형대수학] 선형 방정식과 벡터
안녕하세요!!
@chosungyun입니다.
저번시간에 echelon form이라는 특수한 matrix form에 대해서 소개해드렸습니다.
앞으로 배우는 내용들에 있어서 이 matrix가 많이 사용됩니다. 그래서 가장 먼저 소개해드렸습니다. 그리고 오늘은 선형 방정식에 대해서 소개하고자 합니다.

방정식
“무엇은 무엇이다” 의 꼴을 나타내는 어떠한 값과 어떠한 값이 등식 즉, 같은 관계에 있는 관계에 있을 때 방정식이라 할 수 있습니다.
예를 들어
5x+7y+3z=0 이라는 식이 있다고 생각해보세요. x, y, z는 미지수입니다. 잘 이해되도록 사과, 배, 귤이라고 하죠. 사과에 5배와 배의 7배 그리고 귤의 3배를 더하면 0이 되야 합니다. 이때 사과, 배, 귤은 모두다 없을 수도 있고 혹은 사과는 두개가 있고 배는 하나가 빼앗겨서 -1개이고 귤이 1개가 있다면 또 합은 0이 됩니다. 이러하듯 이 등식관계를 만족하는 미지수의 값을 해(solution)라고 합니다. 이 해는 없을수도, 오직 하나일수도 또는 여러 개일수도, 많을수도 있습니다. 식의 관계에 따라서 말이죠.
선형
선형은 linear하다라고 표현합니다. 이 선형성은 제가 무엇을 배우는 학문인가요? 에서 간단히 소개한바 있습니다.
우리가 앞으로 다룰 거의 모든 주제는 이 선형성을 따릅니다.
위에 예시로든 문제도 선형 방정식입니다. 따라서 선형방정식은 기본적으로 다음과 같은 꼴을 가지고 있습니다.
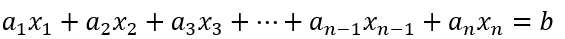
여기서 a와 b는 계수이고 x가 미지수 입니다.
여기서 우리는 선형성을 따르는 방정식이냐 아니냐를 구별해내야 합니다.
선형 방정식
처음에 소개했던 예제를 떠올려 봅시다. 좌변에는 미지수를 포함한 식이 나오고 우변에는 0이라는 숫자가 나왔습니다. 그리고 이 방정식이 선형 방정식이라고 말했습니다.
선형방정식은 간단하게 말하면 일차방정식이라고 할 수 있습니다.
즉, 차수가 1인 미지수들의 선형결합으로 이루어진 방정식입니다.
따라서 미지수들의 곱이 있는 항이 있다던가 루트값인 미지수가 존재한다면 이 방정식은 선형 방정식이 아닙니다.
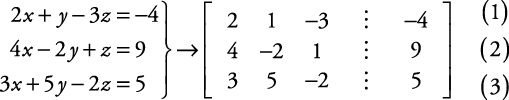
이 선형방정식들이 여러 개 있으면 우리는 해를 구하기 위해 연립방정식을 통해 문제를 풀었었고 이를 선형대수학에서는 coeffcient matrix로 계수들로 이루어진 matrix로 만들어 앞서 소개한 echelon form을 이용해 해를 구하게 됩니다.
자 이제 관점을 조금 달리해서 이 선형방정식을 벡터 개념을 통해 접근해서 보겠습니다.
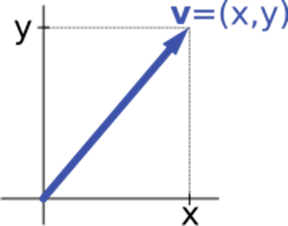
벡터
앞서 포스팅한 벡터와 스칼라 에서 벡터는 방향성을 가진 값으로 설명을 했었습니다.
이제 하나의 벡터가 아닌 두개의 벡터가 있다고 합시다.
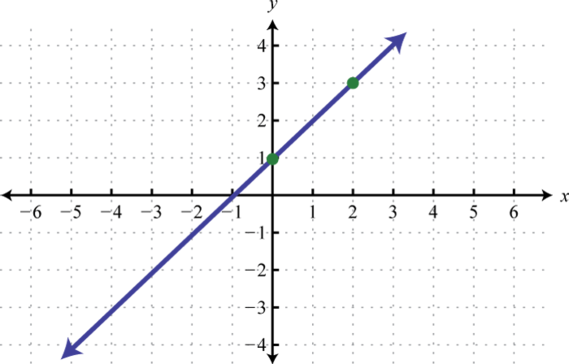
하나의 벡터는 오른쪽으로 한걸음을 이동한 (1,0) 이고 하나의 벡터는 위쪽으로 이동한 (0,1) 입니다. 여기서 오른쪽으로 한걸음 위쪽으로 한걸음 이동하면 (1,1)이 되겠죠?
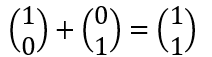
이러하듯 벡터의 합은 각각의 성분끼리 더해주는 결과로 나오게 됩니다. 이는 단 두개의 결과뿐만 아니라 여러 벡터의 합을 모두 더해주는 결과도 동일하게 나타납니다.
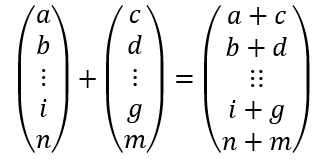
그런데 이러한 결과를 그림으로 그리면 어떻게 될까요?
아래 그림처럼 각각의 벡터 성분의 합으로 어떤 값을 구할 수 있습니다.
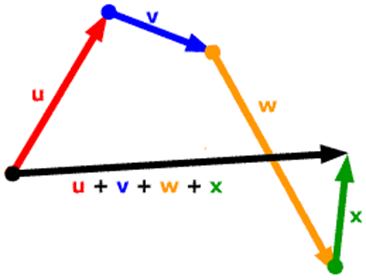
하나씩 주어진 벡터들을 더해가다 보면 결국 하나의 벡터값으로 결과가 나옵니다.
여기서 각각의 column vector(열벡터)를 선형 방정식의 미지수라고 생각해보세요.
u+v+w+x를 하면 검은색 선이 나옵니다. 다시 써보면
u+v+w+x=? 의 결과이죠.
형태가 앞의 방정식과 똑같지요?
이제 2차 함수와 1차함수를 가져와서 보겠습니다.
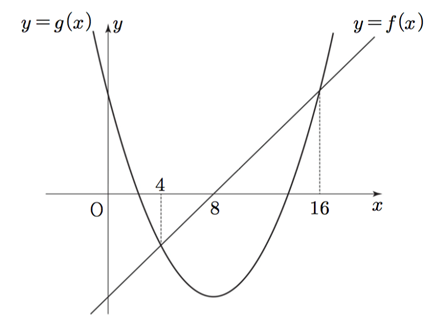
여기서 위그림의 좌표는 지워버리고 그림만 보았을 때 1차함수는 직선이니까 벡터라고 표현할 수 있을텐데 2차함수는 벡터라고 표현하기에는 문제가 많아 보입니다. 그렇기 때문에 이들은 선형결합으로 계산할 수 없습니다. 벡터합이 아니기 때문이죠.
따라서 우리는 벡터들은 선형결합을 이룬다고 하고 선형방정식을 풀수있게 됩니다. 벡터를 적용해서 푸는 만큼 공간적인 해석을 추가하여 이해할 수 도 있습니다.
다음시간에는 이 선형결합으로 나타나는 선형방정식 Ax=b라는 꼴에서 가지는 특징들과 개념들을 알아보겠습니다.
여기서 포스팅을 마칩니다. 감사합니다!!
“해당 포스팅에 사용한 이미지는 구글 이미지입니다”

스스로 홍보하는 프로젝트에서 나왔습니다.
오늘도 좋은글 잘 읽었습니다.
오늘도 화이팅입니다.!
오늘도 감사합니다!!ㅎㅎ
많은 분들이 이런글들을 좀 많이 써주시면 좋겠는데 다수가 관심이 없으니 좀 안타깝네요 ㅜ.ㅜ
저라도 조막손 보팅하고갑니다..
@gillime 님이 관심가져주시니 감사합니다ㅎㅎ
보팅도 감사합니다!^^
다음번에는 Rank나 Nullity 등의 개념이 나오는건가요? 기대하겠습니다 :)
바로는 아니지만 나올 예정입니다ㅎㅎ
기대해주셔서 감사합니다!^^
어려워 지고 있써요 ^^
앞으로 조금씩 더어려워질 예정입니다....ㅠㅠ
그래도 항상 봐주셔서 감사합니다!ㅎㅎ
이전에 봐왔던 개념들이 총출동한 것 같네요 ㅎㅎ 몰라도 열심히 봐두길 잘한것 같은? ㅎㅎ
그렇죠?ㅎㅎ 열심히 봐두셨다니 감사합니다!ㅎㅎㅎ