[수학] 직관적 비교에서의 오류 - 심슨의 패러독스
안녕하세요! ryanhan입니다.
오늘은 통계수치를 직관적으로 비교할 때 생길 수 있는 오류중 하나인
심슨의 패러독스를 소개해보겠습니다.

심슨의 패러독스
A학교와 B학교가 있습니다.
남학생들의 수능 평균점수를 비교했을 때, A학교가 B학교보다 10점 높습니다.
여학생들의 수능 평균점수를 비교했을 때, A학교가 B학교보다 10점 높습니다.
두 학교에서 전체학생의 수능 평균점수는 어디가 더 높을까요?
또, 10점 더 높을까요 ?
남학생과 여학생의 비율
위 문제를 아무 의심없이 보신 분은 전체학생의 평균점수도
A학교가 B학교보다 10점 높을 것이라고 생각하셨을 겁니다.
이것은 남학생 : 여학생 비율이 두 학교에서 같을 때의 계산입니다.
남학생: 여학생 비율이 다를 수 있다는 걸 생각해봤을 때도
언뜻 보면 전체 평균을 봤을 때 여전히 A학교가 B학교보다 높을 것 같습니다.
하지만, 그렇지 않습니다. 남학생 여학생 비율이 극단적이라면
B학교가 A학교보다 평균점수가 높을 수 있습니다.
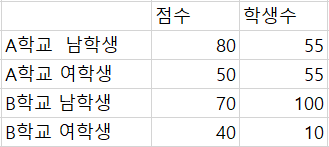
극단적인 예시
위의 표와 같이 남학생 : 여학생의 비율이
A학교에서는 1 : 1 , B학교에서는 10 : 1 이라고 가정해보면,
남학생의 평균점수는 A학교가 10점 높고
여학생의 평균점수도 A학교가 10점 높지만,
A학교의 전체평균 점수는 65점이고
B학교의 전체평균 점수는 67점으로
B학교의 평균점수가 A학교보다 높아질 수 있는 것입니다.

고찰
심슨의 패러독스는 요약하자면,
부분끼리의 비교에서는 항상 큰 값을 가져도
전체에서의 비교는 더 작은 값을 갖을 수 있다는 것입니다.
심슨의 패러독스는 언제 발생할까요?
극단적인 비율을 가지고 있을 때 발생할 것입니다.
실생활에서 예를 들면, A지역과 B지역의 땅값을 비교할 때
A지역의 빌라가 B지역의 빌라보다 비싸고
A지역의 아파트가 B지역의 아파트보다 비싸다고 해서
A지역의 땅값을 B지역의 땅값보다 비싸다고 결론 지을 수 없습니다.
이처럼 심슨의 패러독스는 문제로써 접할 때는
'당연히 비율을 고려해야지!'라고 생각을 하더라도
실생활에서는 자연스럽게 잘못된 논리를 펼칠 수 있습니다.
그래서 우리는 항상 통계를 다룰 때 주의하여야 합니다!
오늘은 심슨의 패러독스를 다뤄봤습니다.
재미있으셨나요??
읽어주셔서 감사합니다.
ryanhan이었습니다!
@clarkgold 님의 이벤트에 당첨되어서
1일1포스팅을 또 기분좋게 하게되네요 ㅎㅎㅎ
감사합니다.
스스로 홍보하는 프로젝트에서 나왔습니다.
오늘도 좋은글 잘 읽었습니다.
오늘도 여러분들의 꾸준한 포스팅을 응원합니다.
앞으로는 무언가를 판단할 떄 라이한님의 글을 보고
다시 한번 생각해서 오류를 예방해 봐야겠습니다 ㅎㅎ
좋은 글 감사합니다!
hanter kim님 안녕하세요!
이 오류는 항상 생각하고 있지않으면
자연스럽게 틀린 결론을 내게 되서
정말 주의해야합니다!!
감사합니다.
역시 통계는 어렵네요ㅠ ㅋㅋㅋ 아무 생각없이 그냥 지나치는 것들이 참 많은 것 같아요. 그런 함정에 속으면 결과적으로 선동당하게 되는 경우도 생길 것 같습니다. 좋은 글 잘봤습니다~~
Coldbeec님 안녕하세요!
맞습니다. 이 경우는 특히 부분을 모아서
전체를 봤을때 결과가 뒤집힐수도 있기때문에 관심을 갖고 봐야합니다!!
찾아주셔서 감사합니다
헐.... 이건 당연히 A 학교가 평균이 높아야 할 것 같은데... 정말 신기하네요. @ryanhan 님의 하시는 일이 궁금한 대목이네요. ㅎ
그쵸ㅎㅎㅎ. . 당연히 A학교가 높을것같다고 저도 생각했습니다. 저는 그냥 대학생이예욤ㅎㅎㅎ.....
10점이 높다만 알려졌을뿐 절대점수가 나오지 않아서 생기는 오류인거 같습니다. ^^ 통계는 정확하지는 않은 수학이나... 그래도 대체적인 경향을 알 수 있다는 점에서 재미난 학문이죠
ㅎㅎㅎ사실 극단적인 절대점수 차이가 있었기에 가능한 예시입니다! 통계가 정확하지 않다는점때문에 많은 머리에서 많은 오류가 생기는것같습니다ㅋㅋㅋ. 그런점들이 재밌어서 한 번 소개해봤습니다. 감사합니다!
아이러니하네요~ 왜그런거지 계속 생각했어요
안녕하세요! 이런결과가나올수있었던 이유는
남학생점수가 여학생점수보다 높고
두 학교에서 남, 여 비율이 극단적으로 차이나기때문입니다!! 실제로 이런경우는 잘 없죠ㅎㅎㅎ
이래서 확률과 통계가 어려운거군요...
ㅋㅋㅋ 확률과 통계과목은 약간 실수하기가 쉬운 것 같아요. ㅎㅎㅎ
이렇게 혼동하기가 쉬우니까요~~~
그래서 더 재미있지 않나요???ㅎㅎㅎ
통계가 일상에서 흔히 접하는 학문이라는 것을 오늘 또 느끼고 갑니다 ㅎㅎ
kimlab님도 연구원 이시니 많이 사용하실 것 같아요 ㅎㅎㅎ
바쁘실텐데 항상 찾아주셔서 감사합니다~~!
맞아요. 비교변수들의 공통기준부터 잘 셋팅을 해놔야 제대로 통계가 돌아가겠죵ㅠ 다만 문제는 실생활에서 같은 비율의 변수들을 찾기란 너무 어려운것..!!! 표본집단부터 추출하고 비교대상들을 선정하는 과정들, 자료찾기가 가장 어렵다고들 하는데 오늘 @ryanhan님의 글을 읽고 생각났어요