투자 계획을 세우는데 필요한 법칙 - 72의 법칙
금융 시장에는 수많은 법칙이 존재합니다. 그중 너무 복잡해서 일반인이 사용하기에는 불가능한 것들이 있는가 하면, 간단하게 적용할 수 있는 것도 있습니다.
후자의 경우가 "72의 법칙"입니다. 복잡한 계산이나 금융 지식도 필요없습니다. 72의 법칙은 투자 원금이 두 배로 되는 데 걸리는 시간을 알려줍니다. 연간 기대 수익률, 이 하나만 정해 놓으면 됩니다. 그리고 72를 연간 기대 수익률로 나누면, 그 값이 바로 투자 원금을 두 배로 불리는데 필요한 시간입니다.
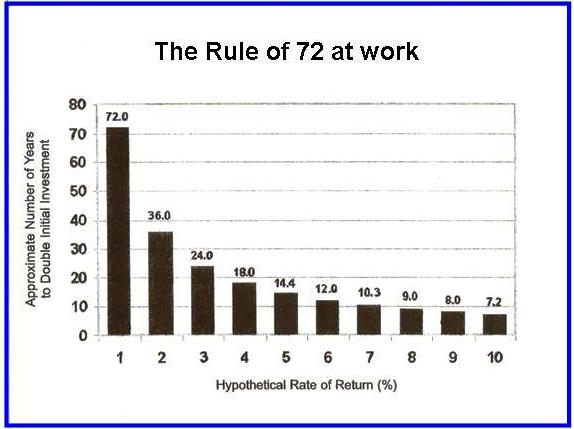
예를 들어, 지금 제게 1백만원이 있다고 하죠. 이 돈을 연간 6%의 이자를 지급하는 곳에 투자합니다. 72의 법칙을 적용해 계산해 보면, 이 돈이 2백만원이 되기까지 12년 (72 ÷ 6 = 12)이 걸린다고 합니다.
"72의 법칙은 투자 원금이 두 배로 되는 데 얼마나 걸릴지를 알려줍니다."
72의 법칙의 응용
투자 비교
72의 법칙의 응용 방법 중 한 가지 분명한 것은 여러 투자에서 원금을 두 배로 불리는데 걸리는 시간을 비교해 보는 것입니다. 각각 우리나라 3년 만기 국채와 코스피 200 지수에 1백만원을 투자한 경우를 비교해 보겠습니다.
최근 기사를 검색해 보면, 현재 3년 만기 국채 금리은 2.282% 수준이며, 지난 10년 간 코스피 지수의 연평균 수익률은 4.5%입니다. 이 두 수치를 기대 수익률로 사용하겠습니다.
1백만원이 2백만원으로 두 배가 되는데 예상되는 기간
3년 만기 국채: 31.55년
코스피 지수: 16년
코스피 지수가 평균 수준을 유지하면, 16년마다 투자 원금을 두 배로 불릴 수 있습니다. 반면, 국채 투자는 주식 대비 훨씬 낮은 변동성과 위험도 작지만, 국채에 투자해 원금을 두 배로 늘리는 데는 31년 이상 걸리게 됩니다.
하지만 여기에는 물가 상승률은 고려하지 않았습니다. 지금의 2백만원과 31년 후의 200만원의 가치는 엄청난 차이가 있을 겁니다. 연평균 물가 상승률을 2%로 가정하고계산을 다시 해 보겠습니다. (2017년에 전국은 1.9%, 서울은 2.0% 상승하였습니다.)
물가 상승률을 감안해, 1백만원이 "진짜" 200백만원이 되는데 예상되는 기간
3년 만기 국채: 255.32년
코스피 지수: 28.8년
"물가 상승은 채권의 최악의 적"이라는 시장의 오랜 격언이 맞군요. 여기서 끝으로 물가 상승률 및 72의 법칙과 관련된 문제를 알아보도록 하겠습니다.
물가 상승률의 영향
72의 법칙은 투자 원금이 두 배가 되는데 걸리는 기간을 알려줄 뿐만 아니라, 현금을 돼지 저금통에 넣어두거나, 장판 밑에 보관할 경우, 그 가치가 절반으로 줄어드는데 걸리는 기간도 알려줍니다. "72 ÷ 물가 상승률"로 계산하면 됩니다.
즉, 물가 상승률을 2%로 가정할 때, 현금을 돼지 저금통에 넣어두거나, 장판 밑에 보관할 경우, 1백만원의 가치가 절반으로 줄어드는 기간은 36년(72 ÷ 2) 입니다. 물가 상승률이 연평균 6%로 상승하면, 1백만원은 단 12년(72 ÷ 6) 만에 가치가 절반으로 줄어들게 됩니다.
이와 같이 72의 법칙은 명목상의 조건과 실질적인 조건(물가 상승률 감안) 하에서 투자 계획을 세우는데 도움이 될 수 있습니다.
읽어 주셔서 감사합니다!!
그렇네요 진짜.. 물가상승률에 대한 감을 쉽게 잡을 수 있겠어요 감사합니당!!
반대로도 됩니다. 10년 안에 원금을 두배로 불리고 싶으면 연간 7.2%(=72/10)가 됩니다.
와... 그럼 여기 나와있는 이야기로는 100만원은 두배불려도 100만원의 가치밖에 지니지 않게되는군요 ㅠㅠ 좋은 글 감사합니다
실은 의심이 많아서
이과라복리계산을 따로해봤는데 잘 들어맞는군요! 잘 활용해보겠습니다!72의 법칙..
저는 72가지의 법칙이 있는줄알고 들어왔다가 ㅎㅎ
72의 법칙을 예제로 드시면서 알기쉽게 설명햐 주셨습니다 감사합니다
특히 원금과 물가상승률과의 관계 재밌습니다 편안한 일밤 보내세요 샘
72=2^33^2
72, 36, 24, 18, 14, 12, 10, 9, 8, 7 ,6 ,5 ,4, 3, 2, 1
7+2=9, 72=14
72/interest = time to double profit
72/rate of inflation = time taken to half the value