1.1 Group Theory (군론)- What is a Group? (군이 무엇인가?)
Introduction
저는 대수기하학 및 정수론 을 블로그에서 심도깊게 다루는 것을 최종 목표로 하고 있습니다.
내용이 어렵기도 하고 다양한 수준의 독자들을 고려해야 하기 때문에 기본적인 대수학 강의를 먼저 할 예정입니다. 위에 언급한 분야들을 연구하기 위해서는 선형대수학, 실해석학, 복소해석학, 대수학, 위상수학, 미분기하학 등의 선수 지식들이 필요한데, 필요하다면 위상수학 정도는 포스팅 해 드릴수 있습니다. (하지만 그림 그리기 귀찮아..)
강의글을 쓸 때 증명을 정말 세세하게 할지 생각했는데 생각해보니 의미가 없는거 같아요. 어짜피 공부는 책으로 하는거고 좋은 reference 들이 많으니.. 그래서 수학 토막상식 (이라고 하기엔 어려울지도..)을 전달하고 수학적 흥미를 유발한다는데 의미를 두고 포스팅을 할 것 같아요.
Steemit Markdown은 Latex 가 지원이 안되네요.. 왠만한 equation 이나 statement 는 그냥 특수문자로 쓰고, diagram 은 Latex 코드를 이미지 파일로 rendering 해서 첨부 할거에요.
잡설이 길어지네요. 아무튼 시작합니다.
본론에 들어가기 앞서:
수학에 관심이 있다면 영어를 잘하는게 중요하거든요. 좋은 reference 들은 죄다 영어, 프랑스어, 등등.. 외국어를 잘하는게 중요해요. 그래서 우선 영어로 설명하고 한국어로 후술 하는 방식으로 할게요.
일단 독자분들이 function (함수) (sometimes it is called a map or mapping. 저는 map 이라는 표현을 더 좋아해요) 이나 set (집합) 이 뭔지 알고 있다고 가정할게요.
∃ 는 'there exists (~가 존재한다,존재해서)', ∀ 는 'for all (모든 ~에 대해서)' 이라는 뜻이고, s.t. 는 such that 의 축약어 입니다.
What is a Group?
일단 독자분들이 function (함수) (sometimes it is called a map or mapping. 저는 map 이라는 표현을 더 좋아해요) 이나 set (집합) 이 뭔지 알고 있다고 가정할게요.
오늘은 대수학의 기본중의 기본인 Group theory (군론)에 대해서 강의를 하겠습니다. 수학 물리 등등 많은 분야에서쓰이는 개념입니다. 오늘은 Group (군)의 정의와 간단한 예시를 배워봅시다.
자, Group을 정의 해 보겠습니다.
Definition of a Group:
이게 무슨 소릴까요.. 벌써부터 혼란스러운 독자분들을 위해 각각의 항목에 대해 설명 드리겠습니다. 첫번째로,
A set G with a binary operation · : G×G→G
라는 표현이 있는데요, binary operation · : G×G→G 이라는 것은, 집합 G 위에서 이루어지는 이항연산(두개의 항을 연산한다)을 의미해요.
(G×G 는G의 Cartesian product 입니다. 쉽게 말해서 G의 모든 순서쌍(ordered pair)들의 집합이죠.)
G×G={(a,b)| a,b∈G}
다시 말해서, '이항연산'이라는 표현은 집합 G에 있는 '두개의 원소'를 뽑아서 연산을 하면 G에 있는 '하나의 원소'가 된다는 것이에요.
쉬운 이해를 위해 예시를 들어볼게요. ℤ를 모든 정수들의 집합으로 정의하고,
ℤ={···,-2,-1,0,1,2,···})
+ 를 우리가 잘 알고있는 덧셈 (usual addition) + 로 정하겠습니다. + 는 두개의 숫자를 더하는 연산이죠. 다시 말해서 두 숫자의 순서쌍을 다른 숫자로 보내주는 함수입니다. 그러면 +는 ℤ×ℤ 위에서 정의된 ℤ로 가는 함수가 되고 따라서 ℤ 위에서의 이항연산이 되죠. 예를 들어, +는 (2,3)을 5로 보내줍니다. (2+3=5 의 재해석..)
마지막으로 위의 Group 정의에 나와있는 1, 2, 3번 조건들은 각각 결합법칙, 항등원의 존재성, 역원의 존재성 인데요, 다들 고등학교 수학시간에 배웠으리라고 생각해서 자세한 설명은 안할게요.
이것도 마찬가지로 예시를 들어서 설명하는게 이해가 빠를거 같아요. 위에서와 마찬가지로 ℤ에 대해서 생각해 보죠. 정수 a,b,c∈ℤ 에 대하여
(a+b)+c=a+(b+c) (결합법칙; 예: (2+3)+5=2+(3+5)=10)
0+a=a+0=a (덧셈에 대한 항등원은 0; 예: 0+2=2+0=2)
a+(-a)=(-a)+a=0 (a의 역원은 -a; 예: 3+(-3)=-3+3=0)
가 성립하는 것을 알 수 있습니다.
Group (군)의 정의를 끝내기 전에, 몇가지 알아야 할 사실들을 짚고 넘어갈게요 (Remarks):
Remark
G 가 연산 ·에 대하여 Group 이라고 하겠습니다. (또는, 이를 "(G,·) 이 Group이 된다"고 간략하게 쓰기도 합니다) 그럼 다음이 성립합니다:
G의 항등원 e는 유일합니다 (e' 가 G의 또다른 항등원이라면, e=e' ).
각각의 원소 a∈G 에 대하여 역원 a^{-1}는 유일합니다.
(둘 다 쉽게 체크 가능)
Notation (표기법)
이항연산을 덧셈 +로 쓰면 +에 대한 역원(Inverse)는 -a 로 쓰고 (additive notation),
이항연산을 곱셈 ·으로 쓰면 · 에 대한 역원은 a^{-1} 로 주로 씁니다 (multiplicative notation).
(2의 덧셈에 대한 역원은 -2이고, 3의 곱셈에 대한 역원은 1/3이라고 표기하는 것을 생각해보세요. 당연하죠.)
Remark
위에서 살펴본 바로 알 수 있듯이 모든 정수들의 집합 ℤ는 연산 +에 대해서 군이 됩니다! 이때 (ℤ,+) 가 군이 된다고 표현합니다.
자, 생각보다 군은 쉽습니다, 유치원 때 부터 배워왔고 우리 생활 가까이에 있다는걸 알 수 있죠. 하지만 수학을 심각하게 공부해보면 어려운 군들이 많습니다.
다음 시간에는 군의 쉬운 예제들을 몇가지 들어보겠습니다.
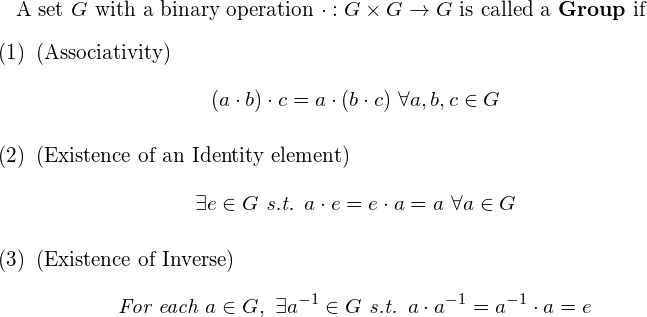
잘 읽고 갑니다. 평소 대수학 쪽에 관심은 있었으나 혼자 공부할 엄두가 안나서 공부를 못하고 있었는데 앞으로 종종 들리도록 하겠습니다. 팔로우 했습니다!
팔로우 감사합니다 ~ 좋은 포스팅 많이 올리겠습니다!
선형대수부터 포기한 수포자입니다.. orz
팔로우하고 다시 한번 공부를 시도해 보겠습니다!
선형대수도 사실 module theory의 특별한 경우라.. 제 포스팅 따라오신다면 좋은 결과가 있을거에요. 질문 언제든 편하게 남겨주세요!