4-4 TensorFlow Numerical Analysis Revival: sin(x) = 0

이미 TensorFlow를 사용하여 2차 방정식을 비롯한 다항식 형태의 방정식들을 대상으로 cost 함수를 설정하여 경사하강법에 의해서 해를 구할 수 있었으며 상당히 많은 사례들이 2018년 말에 출간했던 필자의 졸저의 5장에서 찾아볼 수 있다.

머신 러닝 수치해석 편에서 다루는 수학 방정식들의 풀이 대상 문제는 불과 13종류에 불과하나 중학교 수준에서 시작하여 대학 및 대학원 수준까지의 모든 문제들을 망라했다고 볼 수 있다. 이와 같이 머신 러닝에 의한 수학 방정식의 해법을 다루게 된 동기는 이미 Mathematica 와 같은 수학소프트웨어를 활용하여 방정식을 풀 수 있긴 하지만 그 바닥에 깔려 있는 해법이 무엇인가 하는 문제에 대한 의구심에 출발한다.

특히 비선형 방정식들에 해법으로서 Newton Raphson Method 에 주목하지 않을 수 없다, 이 방법에 의해서 웬만한 방정식의 해는 다 구할 수 있으나 항상 초기 값을 부여해야 하는 너무나 불편한 점을 지적하지 않을 수 없다. 특히 주기함수의 경우에서처럼 여러 개의 해가 되풀이 될 경우에는 되풀이 되는 경우의 수 만큼 초기 값을 주어야 하는 번거로움이 뒤따를 수밖에 없으며 결국 Mathemaica도 주어진 범위 내의 해를 전부 찾아 주는 건 사실이지만 내부적으로 Newton Raphson Method가 아닌 특출한 알고리듬을 사용하지는 않는 것으로 보인다.

반면에 머신 러닝에서의 방법론은 항상 간단한 학습을 시킨 후 적절한 Hypothesis 함수를 구성함과 아울러 학습된 내용과의 에러 차이를 바탕으로 cost 함수를 구성하여 에러를 최소화 시킬 수 있도록 경사 하강법을 적용하는 것이다.

머신 러닝의 우수성은 졸저의 5장 10절에서 방정식 사례에서처럼 Newton Raphson Method가 풀지 못하는 경우까지 다 풀어내는 막강함을 보여 주기도 한다. 한편 이미 2018년 말에 출간했던 필자의 졸저에서 비선형 삼각함수 방정식인 sin(x) = 0 에 대해서 Newton Raphson 수치해석법이 아닌 TensorFlow 에 의한 Hypothesis 함수 구성법과 해법을 선 보였으나 이번 블로그에서는 변형된 보다 간편한 Hypothesis 구성 방법을 시험해 보기로 하자.

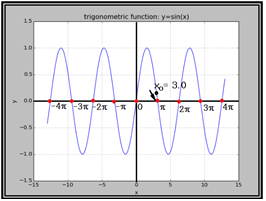
삼각함수 방정식 sin(x) = 0 은 비선형 형태의 방정식으로서 해가 위 그림에서처럼 x=∓nπ, n=0,1,2,3,... 으로 주어지는 sin(x) = 0 의 해는 다음과 같이 infinite product 형태의 표현식으로부터 직접 얻을 수도 있음을 참조하자. 미적분학을 공부했으면 특정 함수들이 Maclaurin Series 형태로 급수 전개가 가능하다는 점을 상식적으로 알고 있을 것이다. 하지만 infinite product 형태의 함수 표현은 인도출신의 수학 천재로 알려졌던 Ramanujan 같은 수학자만이 즐겨 쓰는 함수 표현 방식임을 참고하고 이로부터 영감을 받아 머신 러닝 방식에 의해 해를 구해 보자.

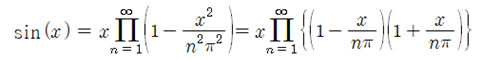
Ramnujan 같은 절세의 수학자가 풀어준 위와 같은 형태의 함수 표현을 본다면 누구든지 쉽게 그 해가 0 또는 ∓nπ 임을 알 수 있다. 하지만 수치해석에서 그와 같은 절묘한 해법을 기대하기는 난망이다. 그냥 무식하게 주어진 함수에 대해서 해를 찾아야 하는 것이다.

한편 Newton Raphson 기법에 의한 수치적인 해를 얻기 위해서는 해가 있을 법한 위치 근처에서 초기 값 를 설정해야 한다. 구체적인 실례로서 = 3.0 으로 두자. 이 값을 사용하여 Newton Raphson의 반복법에 의해 근접한 해를 구할 수 있다.

반면에 TensorFlow를 사용하여 해를 구하기 위해서 적합한 cost 함수를 설정하도록 하자. 즉 n차 다항식 형태의 함수의 해를 찾기 위한 cost 함수의 설정을 참고하면 찾고자 하는 해의 수만큼의 웨이트(weight) 들을 변수로 도입하여 곱하기 형태로 아래와 같이 Hypothesis를 설정할 필요가 있었다.

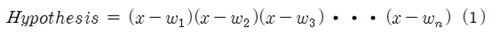
이러한 방법은 특히 다항식 형태의 방정식에 적합하다.

마찬가지로 -nπ ≤ x ≤ nπ 구간에서 y = sin(x) 의 해 2n+1 개를 구하기 위해서는 필자의 졸저에서 아래와 같이 비선형 형태의 Hypothesis를 설정하였다.

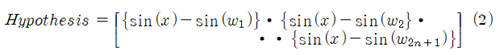
하지만 이번에는 좀 다른 형태의 아래와 같은 Hypothesis를 시도해 보기로 한다.
구체적인 수치 계산 사례로서 x= -π, 0, +π 3개의 해를 가지는 경우를 고려해 보자.

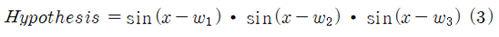
(3)식 형태의 Hypothesis 가 (2)식 보다 더욱 간단해 보인다.

3개의 weight들 즉 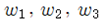는 그림과 같이 3개의 구간으로 나누고 초기 값으로는 난수 값을 부여하도록 하자.

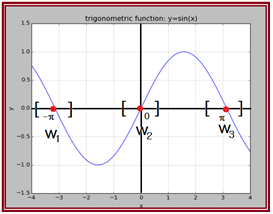
TensorFlow에서 초기 값을 부여하기 위한 명령으로는 tf.zeros(), tf.ones(), tf.random_normal() 및 tf.random_uniform()을 포함하는 방법들이 있는데 여기서는 random_uniform()을 아래의 일례에서처럼 적절한 구간 지정과 함께 사용하기로 하자. 이 범위는 직접 함수를 matplotlib 르 사용하여 작도해 보고 대략적으로 해를 포함하도록 여유 있게 구간을 잡되 서로 중복됨이 없도록 하자.

이 구간 지정에서 한쪽은 닫힌 형태임에 반해 다른 쪽은 열린 형태인데 이는 TensorFlow 의 구간설정 문법특성에 따른 것임을 지적해 둔다.

아울러 경사하강법을 적용하기 전에 함수를 정해진 구간 내에서 학습을 시키도록 하자. 그림에서 관찰할 수 있듯이 함수 형태는 3개의 해를 가지는 3차 다항식 함수와 유사하다. 3차 다항식을 정확하게 규정하기 위해서는 4개의 점 좌표가 필요하므로 여기서도 4개의 점 좌표를 준비하도록 한다. 이 점 좌표는 앞서 정의 된 weight 들의 초기 값을 부여하기 위한 구간 설정과는 아무런 상관이 없으며 고려하는 전체 구간을 대상으로 함수 즉 를 가장 적절히 표현할 수 있는 점들의 데이터를 준비하는 것이 바람직하다.

아울러 학습 데이터 양을 다음과 같이 4가지 경우를 고려해서 실행해보자.

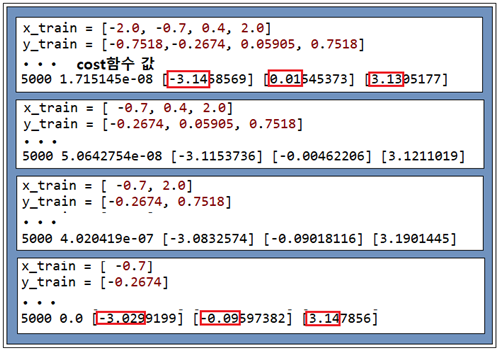
물론 MNIST 숫자 인식 문제에서처럼 학습 데이터 수가 어느 정도 많을수록 정확한 해를 구할 가능성이 높을 것으로 예상되나 최소한도의 데이터를 사용해도 몇% 이내의 정밀도를 가지는 해를 실용적으로 구할 수 있다. 아래의 계산 결과는 learning rate = 0.5 일 때의 계산 결과이며 4개의 점 데이터를 사용하여 학습시켰을 경우 1% 이내 수준의 정밀도를 보여 준다. 반면에 학습 데이터량이 적다고 해서 해를 못하는 것은 아니라 정밀도가 떨어짐을 쉽게 알 수 있다.

첨부한 코드를 다운받아 indentation을 확인 복원하여 실행시켜 보자.

#sineqn_regression_02.py
import tensorflow as tf

x_train = [-2.0, -0.7, 0.4, 2.0]
y_train = [-0.7518,-0.2674, 0.05905, 0.7518]
#x_train = [ -0.7, 0.4, 2.0]
#y_train = [-0.2674, 0.05905, 0.7518]
#x_train = [ -0.7, 2.0]
#y_train = [-0.2674, 0.7518]
#x_train = [ -0.7]
#y_train = [-0.2674]

W1 = tf.Variable(tf.random_uniform([1],-3.2, -3.0, dtype = tf.float32, name='weight1'))
W2 = tf.Variable(tf.random_uniform([1],-0.5, +0.5, dtype = tf.float32, name='weight2'))
W3 = tf.Variable(tf.random_uniform([1], 3.0, 3.2, dtype = tf.float32, name='weight3'))

#hypothesis = (tf.sin(x_train) - tf.sin(W1))(tf.sin(x_train) - tf.sin(W2))(tf.sin(x_train) - tf.sin(W3))
hypothesis = tf.sin(x_train-W1)tf.sin(x_train-W2)tf.sin(x_train-W3)
cost = tf.reduce_mean(tf.square(hypothesis - y_train))

optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.5)
train = optimizer.minimize(cost)

sess = tf.Session()
sess.run(tf.global_variables_initializer())

for step in range(5001):
sess.run(train)
if step % 1000 == 0:
print(step, sess.run(cost), sess.run(W1), sess.run(W2), sess.run(W3))