4-1 TensorFlow 머신 러닝의 Back Propagation 기법에 의한 선형회귀 예제

3개의 점 데이터 (1,1), (2,2), (3,3)를 학습을 위한 입력 데이터 x_train 과 출력 데이터 y_train 으로 나누어 코드에서 사용할 수 있는 list 데이터 구조의 형태로 표현하자.

x_train = [1, 2, 3], y_train = [1, 2, 3]

이 데이터 대상으로 y = W*x + b 형태로 hypothesis를 설정하여 cost함수를 구성하고 경사하강법을 적용한 학습에 의해 웨이트 W 와 바이아스 b를 결정하도록 하자. 계산해 보지 않아도 웨이트 W = 1 이고 바이아스 b = 0 이 답이란 점을 알고 시작하기로 한다.

입력 데이터 x_train을 사용하여 계산 되는 hypothesis 값과 y_train 과의 차이 값의 제곱을 합하여 평균한 값인 cost 함수는 머신러닝 과정에서 항상 최소화(minimization)의 대상이 된다.

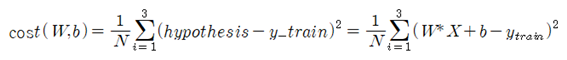
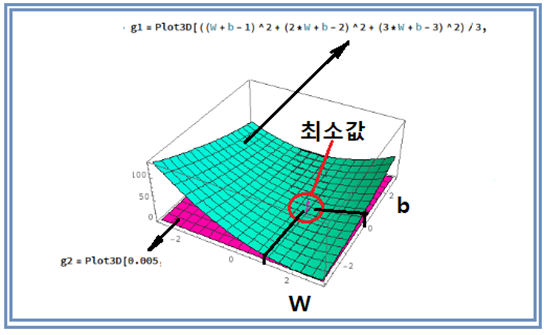
위의 3차원 곡면은 가로축 W 와 세로축 b 의 구간이 각각 (-3,+3)인 범위에서 cost 함수의 3차원 그래픽 형상이다. cost 함수가 최소 값을 가지게 되는 (W, b) =(1, 0) 에서 cost 함수의 값이 0.0 이므로 근사적으로 z = 0.005 인 평면과의 만나는 지점을 겹침을 통해 cost 함수가 최소값을 가지게 되는 근방의 영역을 시각화 하였다.

여기서 웨이트 W 와 바이아스 b는 특정의 방정식을 풀어서 한번에 결정되는 것이 아니고 임의로 지정되는 난수 값에서 시작한다. TensorFlow에서는 tf.random_normal() 명령을 사용하여 초기 값을 설정한다. random_normal의 default 조건에서 평균 값이 0.0 이고 표준편차가 1.0 으로 처리되므로 항상 [-1, +1] 영역 범위 내에서 시작점이 정해진다.

cost함수는 W 와 b의 연속 함수이므로 W 또는 b에 관해 편미분하여 cost 함수의 방향별 기울기(directional derivative)를 계산할 수 있다. 다시 말하면 gradient를 계산할 수 있다는 뜻이다. 즉 weight W 와 바이아스 b는 서로 독립적인 연속 변수로 볼 수 있으므로 각각에 대해서 다음과 같이 편미분에 의해 기울기를 구해 보자.

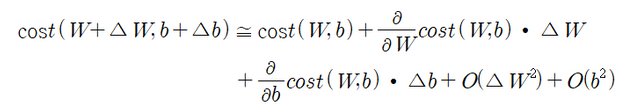
여기서 i 와 j 는 서로 수직한 W 방향과 b 방향의 단위 벡터로 정의 한다.

한편 (W,b) 점에서 미소량 (△W,△b)만큼 움직인 근방(neighbourhood)에서의 cost함수는Maclaurin 급수 전개 이론에 의해 다음과 같이 근사적으로 얻어진다.

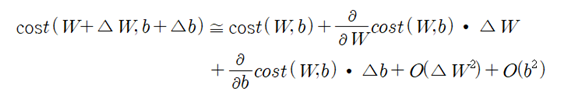
Maclaurin 급수 전개에서 생략된 부분은 cost 함수의 W와 b에 대한 2차 편미분 항을 포함하게 되는데 미소량들의 제곱 항과 곱해지기 때문에 미소량 자체가 충분히 작은 값이라면 그 제곱은 무시할 정도로 작다고 볼 수 있다. 따라서 Maclaurin 급수전개의 1차 항들만 가지고도 (W+△W, b+△b) 점에서의 cost함수 값을 쉽게 계산할 수 있다. 아울러 경사하강법에서의 미소량 (△W,△b)의 값 설정은 다음과 같이 일괄적으로 그 크기가 1.0 보다 작은 하나의 learning rate 값을 사용하여 설정한다.

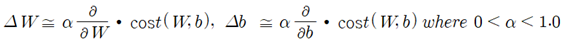
아울러 경사 하강법에서 매 학습횟수 단계별로 수렴해 나가는 cost 함수의 값을 계산할 수 있는데 이 문제의 경우 cost 함수의 최소 값은 (W, b) =(1, 0)에서 0.0이 되어야 한다.
그러므로 경사하강법에 의한 cost 함수의 최소 값을 주게 되는 (W, b) 의 값은 다음과 같이
| cost 함수 – 최소값 |≤ε 이 되는 에러 조건을 적용하여 찾아내도록 한다. 에러의 값은 작을수록 좋으나 반복 학습 횟수가 늘어날 수 있으므로 적정한 크기로 잡도록 한다.

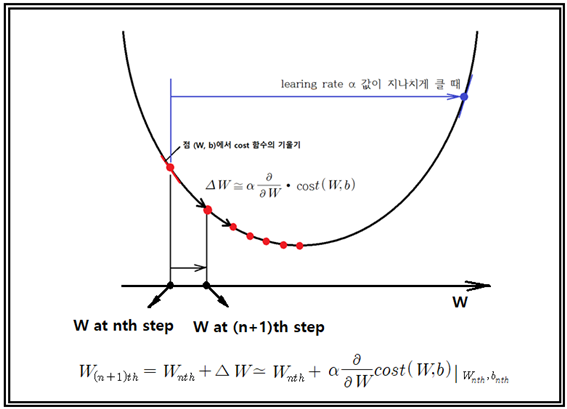
learning rate의 값이 지나치게 크다면 반복되는 step에서의 cost 함수 계산 시 cost 값이 증가하여 발산할 수도 있으므로 그 값을 줄여서 조정해야 한다.
TensorFlow에서 첫 번째 cost 함수 계산에서 W 와 b 값은 tf.random_normal()에 의해 주어지며 그 다음 번부터는 n번째 step 의 (W, b)에서 gradient 계산이 가능하면 cost 함수가 하강하게 되는 (n+1)step 위치를 위 그림의 공식을 참조하여 결정할 수 있다.

충분한 횟수의 반복학습을 통해 cost 함수의 변동이 거의 없이 주어진 에러 한계 이내에 들어왔다고 판단하게 되면 이때의 웨이트 W와 바이아스 b의 값이 최종적으로 확정 된다. 이 방법론 수치해석과 최적설계(Optimization) 분야에서 특히 오래전부터 확립되어 사용하는 기법인데 유독 머신 러닝 분야에서는 전 세계적으로 연구 참여자가 거의 전무했기 때문인 듯 아무도 이 기법을 적용치 않았으며 1980년대에 가서 Hinton (1986)교수가 논문으로 발표했으며 동일한 내용에 대해서 70년대 후반에 Werbos(1974,1982)에 의한 한편의 논문이 있었으나 학계의 무관심과 냉대로 거의 알려지지 않았다고 한다. 이미 타 분야에서는 너무나 뻔한 수치해석 초보 수준의 알고리듬이지만 특히 신경망분야의 발달이 너무나 지연되어서 발생한 현상인 듯한데 (n+1) step 계산을 위해 n step 에서의 편미분 결과를 이용하는 기법을 Back Propagation 이라고 한다.

Back Propagation 기법이 머신 러닝 분야에서 많이 회자되는 이유로는 1969년 Minsky 와 Papert 교수의 공저인 퍼셉트론 이란 책에서 퍼셉트론이 1단 NN을 사용하여 XOR 문제를 해결 할 수 없다는 점을 지적하고 아울러 여러 단의 퍼셉트론을 직병렬 연결하여 풀 수 있는 가능성은 있을 수 있으나 어떻게 웨이트 와 바이아스 값을 업데이트 할 수 있는지 그 방법을 모르기 때문에 풀 수 없는 것으로 단정을 지워버린 내용이 들어있다. 하지만 불과 얼마 안되어 70년대부터 80년대에 걸쳐 컴퓨터의 급격한 발전과 더불어 수치해석과 Optimization( 최적설계엔지니어링 분야에서 발전된 머신 러닝과 흡사한 기법)이 크게 발달하여 그 문제 해결이 가능해졌다.

Back Progation 에 관해서 별도의 계산 예제들이 있기는 하지만 TensorFlow를 사용하게 되면 이미 다 포함되어 있는 내용에 해당한다는 점을 지적해 두자.

특히 TensorFlow 는 TensorBoard 지원 하에 cost 함수의 변화를 그래프로 작성 모니터링 가능하며 컴퓨터에서 실행되는 머신 러닝 코드가 내부적으로 노드(node)와 엣지(edge)로 구성되는 Computational Graph 로 구성되어 있어 경사하강법을 사용하면 Back Propagation 방법으로 계산할 수 있도록 구성이 되어 있다.

아래는 아나콘다 스파이더3에서의 계산 결과 출력 사례이다. step 수가 증가할수록 cost 함수가 작아짐을 볼 수 잇다. 결과적으로 W는 1.0에 b는 0.0에 수렴함을 볼 수 있다.

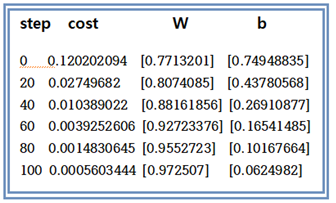
아울러 TensorFlow 연산과정에서 step 에 따른 cost 함수를 plot 해보고 Computational Graph를 관찰하기 위해서는 코드를 TensorBoard 기능을 사용할 수 있도록 다시 재작성해야 한다. 이 기능을 사용하게 되면 별도의 웹페이지가 생성되어 코드의 노드 구조와 cost 함수의 그래프 정보를 모니터 할 수 있다. 별도로 포스팅할 계획이다.

첨부된 파이선 코드를 실행해 보자. 단 session = tf.Session() 이하 영역에서 indentation 이 무너진 부분을 반드시 복구하여 실행하기 바란다
//linear_regression_01.py
#Linear Regression
import tensorflow as tf
tf.set_random_seed(777) # for reproducibility

#X and Y data
x_train = [1, 2, 3]
y_train = [1, 2, 3]

#Try to find values for W and b to compute y_data = x_data * W + b

W = tf.Variable(tf.random_normal([1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')

#hypothesis XW+b
hypothesis = x_train * W + b

#cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - y_train))

#Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.05)
train = optimizer.minimize(cost)

#Launch the graph in a session.
sess = tf.Session()
#Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())

#Fit the line
for step in range(1001):
sess.run(train)
if step % 100 == 0:
print(step, sess.run(cost), sess.run(W), sess.run(b))