3-10 Softmax AND 로직 머신 러닝 hypothesis surface 3차원 그래픽 Visualization
백문이 불여 일견이라 복잡하고 상세히 설명보다는 3차원 그래픽 비쥬얼라이제이션을 통해 Softmax hypothesis 확률 분포 곡면을 관찰해 본다면 Softmax 에 대해 그동안 가져왔던 불투명했던 면을 일거에 깨우칠 수 있으리라 기대한다.
다음의 수치 예제를 통해서 Softmax를 완벽하게 이해하는 계기로 삼도록 하자. 다음의 수치 계산 결과는 AND 로직 계산 결과이다. learning rate = 0.1에 반복학습 횟수를 고의적으로 100회에 한정했다. 반복학습 횟수가 500회를 상회하면 계산되는 확률 값이 거의 1.0 과 0.0 에 가까워 수작업으로 계산해 보기 어렵게 된다. 하지만 100회 계산 결과지만 result를 보면 아울러 hypothesis 값을 보면 threshold = 0.5로 볼 때에 충분히 AND 로직을 시사하고 있음을 알 수 있다.
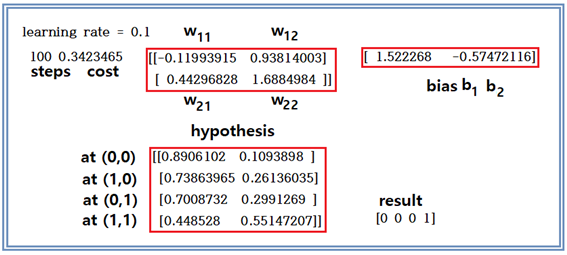
다음은 위 결과를 표로 정리해 놓은 것이다.
AND 로직을 Softmax 기법으로 계산하기 위한 데이터로서 다음 그림을 참고하여 4개의 데이터 (0,0), (1,0), (0,1) a 및 (1,1) 을 리스트 형태로 코딩하여 입력한다. 여기서 “0”과 “1”은 논리 값 즉 “LOW”와 “HIGH”를 뜻하지만 분리선(Classifier)를 찾아내기 위한 좌표값으로 봐도 무방하다.
머신 러닝 학습에 의해 얻어진 웨이트 벡터와 바이아스 벡터를 사용하여 각 좌표 별로 2개의 성분을 가지는 one hot code 라벨 값 성분들의 확률 값을 계산하자. one hot code 라벨 값의 2 성분들은 결국 확률이므로 그 합은 1.0 이 되어야 한다. 이론 적으로는 (1,0)과 (0,1) 이 나와야 하지만 현재 반복학습 횟수가 대단히 적으므로 그 합이 1.0 이면서 어느 한쪽이 0.5 이상이라면 Sigmoid 함수에서처럼 그 쪽을 “HIGH” 또는 “1” 로 판정을 내릴 수 있다.
웨이트 벡터와 바이아스 벡터의 소수이하 자리수가 너무 길어 소수이하 둘째자리까지 반올림하여 취하였다.
이 값들을 사용하여 구체적으로 Softmax 확률 함수의 식을 써보자. 두 확률 성분을 합하면 1.0 이 됨을 쉽게 확인할 수 있다.
그림의 softmax(xi) 확률 정의 식을 참조하여 다음과 같이 분자의 엑스포넨셜 항을 계산하자.
계산된 값을 사용하여 각각의 입력 좌표에서의 라벨 값 확률 성분들을 계산해 보자.
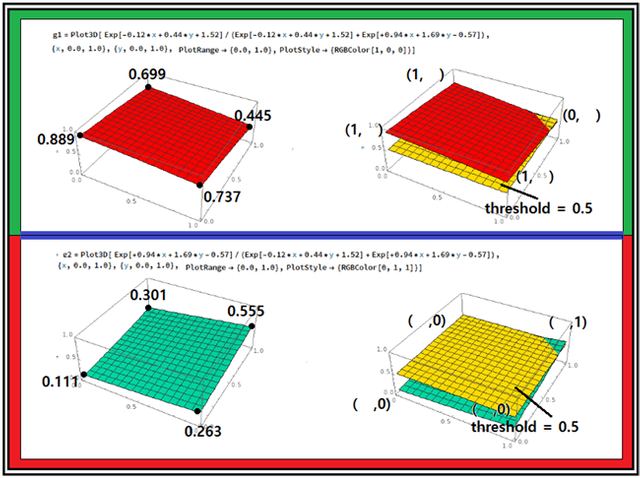
평면상에서 정의 되는 AND 로직 문제를 최종적으로 계산된 확률 값을 대상으로 수치적으로 threshold = 0.5 상회하는지 하회하는지 판단하면 된다. 반면에 Softmax 확률 함수의 식은 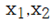 변수의 함수이므로 3차원 공간상에서 threshold 면과 함께 다음과 같이 그래픽에 의한 비쥬얼라이제이션도 가능하다. 즉 두 개의 이벽 변수를 갖는 로직들에 대해서는 두 개의 라벨 값 확률 변수를 가지므로 3차원적으로 비쥬얼라이제이션에 의한 확인이 유일하게 가능하다. 엑스포넨셜 함수 사용에 따라 나타나는 곡면이 상당히 복잡할 것으로 예상했으나 오히려 상당히 매끈하면서도 평탄한 특성을 보여 준다.
변수의 함수이므로 3차원 공간상에서 threshold 면과 함께 다음과 같이 그래픽에 의한 비쥬얼라이제이션도 가능하다. 즉 두 개의 이벽 변수를 갖는 로직들에 대해서는 두 개의 라벨 값 확률 변수를 가지므로 3차원적으로 비쥬얼라이제이션에 의한 확인이 유일하게 가능하다. 엑스포넨셜 함수 사용에 따라 나타나는 곡면이 상당히 복잡할 것으로 예상했으나 오히려 상당히 매끈하면서도 평탄한 특성을 보여 준다.
첨부된 파이선 코드를 실행해 보자. 단 session = tf.Session() 이하 영역에서 indentation 이 무너진 부분을 반드시 복구하여 실행하기 바란다
#softmax_AND_logic_01.py
#Softmax Classifier
from matplotlib import pyplot as plt
import numpy as np
import tensorflow as tf
tf.set_random_seed(777) # for reproducibility
x_data = [[ 0, 0 ], [ 1, 0], [ 0, 1], [ 1, 1] ]
y_data = [ [1, 0], [1, 0], [1, 0],[0, 1] ]
X = tf.placeholder("float", [None, 2])
Y = tf.placeholder("float", [None, 2])
nb_classes = 2
W = tf.Variable(tf.random_normal([2, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
#hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
#cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
#Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(101):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 10 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}), sess.run(W),sess.run(b))
#Testing & One-hot encoding
all = sess.run(hypothesis, feed_dict={
X: [[ 0.0, 0.0 ],[ 1.0, 0.0], [ 0.0, 1.0 ], [ 1.0, 1.0 ]]})
print(all, sess.run(tf.argmax(all, 1)))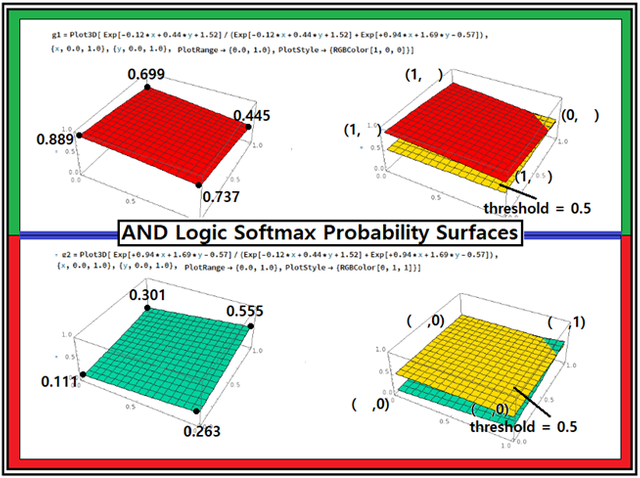

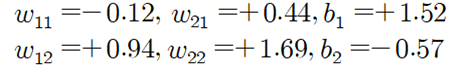
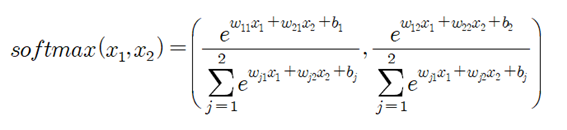
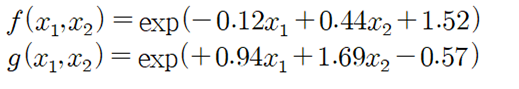

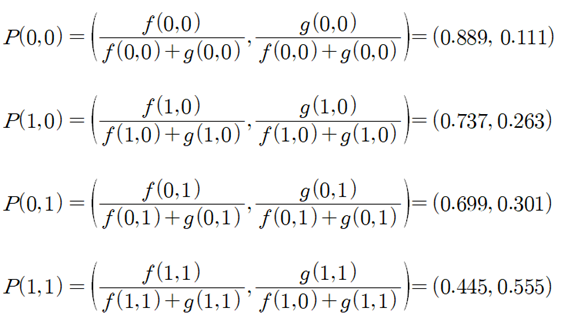
Congratulations @codingart! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOP