2-5 Softmax 에 의한 Hypothesis 확률 계산 개론

MNIST 뿐만 아니라 사진 이미지 머신 러닝을 위한 CIFAR-10 데이타 경우도 각 사물별로 10개씩의 사진 이미지를 학습용 데이터로 제공하기도 한다. 즉 plane 비행기를 하나의 클라스로 잡고 비행기의 특징(feature)을 보여 줄 수 있는 10장의 학습용 샘플로 데이터 베이스를 구성하는 것이다. MNIST 숫자 데이터 베이스가 흑백임에 비해 컬러 처리하는 경우 RGB 만해도 기본 3배 규모로 데이터가 커지는 셈이다. 따라서 MNIST 처럼 한 class 당 5500개의 샘플을 준비하는 것이 불가능하지는 않지만 GPU 장착 컴퓨터를 써야 할지도 모른다. 이런 점에서 아직 우리가 연구하는 머신 러닝이 인간의 지능 대비 격세지감이 느껴진다. 즉 현재 우리가 알고 사용하는 학습 알고리듬! 그다지 잘못 된 건 없어 보이는데 아마도 양자 컴퓨터가 나와야 해결이 될 것인가?

Hypothesis 의 레벨 수가 반드시 10인 것만은 아니다. 분류하려는 데이터 종류 수에 달린 것이다. 아울러 class를 형성할 학습용 데이터 준비에서 중요한 요인은 과연 이 데이터들이 identical 하면서 distinguishable 한 특성을 지니고 있느냐는 문제일 것이다.

MNIST에서는 이 수기 숫자들을 픽셀fh 구성된 이미지화 하여 28X28 매트릭스로 표현하여 TensorFlow에서 사용한다. 이 28X28 샘플 데이터들은 reshaping을 통해 784개의 항을 가지는 1차원 어레이 형태의 입력 벡터 X로 설정이 가능하며 아울러 784X10 웨이트 매트릭스 W의 컬럼들에 대응하게 되는데 1X10 바이아스 매트릭스 b 와 함께 Hypothesis 연산을 하게 되면 실수 값 형태로 다음과 같이 10개의 성분을 가지는 1X10 매트릭스가 얻어진다.

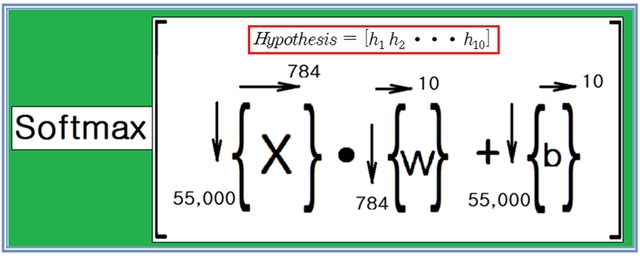
한편 수학적인 편의를 위해서 784개에 “1”의 값을 가지는 매트릭스 요소 하나를 입력 데이터 X의 마지막에 추가하고 웨이트 매트릭스를 785X10으로 구성하면 별도로 바이아스 매트릭스를 고려하지 않아도 된다. 다음 그림을 참조하자.

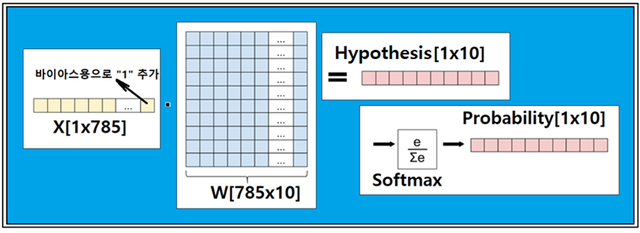
Linear classifier를 사용하는 MNIST문제에서 지도학습 과정은 처음에 identical 하면서 distinguishable한 입력 벡터에 대해서 랜덤한 값의 W 와 b를 생성하여 매트릭스 연산을 시작하게 되면 위 그림의 Hypothesis에서 처럼 1X10 매트릭스 형태로 10개의 랜덤한 계산 값들이 얻어진다. 이때에 사용되는 매트릭스 연산 함수를 Hypothesis라 한다.
머신 러닝에서 Hypothesis 는 class에서 할당하는 one hot code 와 매치가 되어야 하지만 처음에는 입력벡터와 랜덤한 웨이트와의 매트릭스 연산에 얻어지는 임의적인 값을 보여 주므로 설정된 one hot code와 거의 일치하도록 학습(trainning)과정을 거쳐야 한다.

Softmax에서의 학습과정에서는 Cross Entroy라는 cost(loss) 함수로 사용하여 경사 하강법에 의해서 최소화 될 때까지 학습연산이 이루어진다. 한편 TensorFlow를 사용하는 Softmax 문제에서 Hypothesis를 Logits 이라고도 한다.

입력벡터 X와 웨이트 W를 직접 곱하기 매트릭스 연산하여 Hypothesis를 계산하는 기법을 선형 분류법(Lenear Classification)이라고 하며 반면에 이 Hypothesis를 무리수 e 의 지수로 적용하여 확률 처리하는 기법 중의 하나가 볼츠만의 통계 역학 공식을 차용했다고 하는 Softmax 기법이다.

볼츠만 확률 분포에서의 에너지 레벨에 대해 Softmax에서는 특정 클라스에 속하는 MNIST 이미지 데이터(X)에 대한 Hypothesis(=X⦁W)값이 대응하게 된다. 볼츠만의 통계역학에서는 입자들의 평균 운동속도나 평균 에너지 또는 rms 평균속도(root mean squre velocity)가 물리적 관점에서의 통계적 관심 항목들이다. 특히 통계 물리학과 통계학과의 근본적 차이점은 볼츠만의 확률분포는 아예 물리학의 법칙처럼 인식되지만 통계학에서는 항상 데이터를 사용한 모델의 수립과 아울러 테스트를 거쳐야 한다는 점에서 머신 러닝은 방법론 상 물리학적이 아닌 통계학의 범주가 되는 것이다