2-3 Softmax와 볼츠만 확률분포와의 Analogy-III: 볼츠만 확률분포 유도

입자들이 포함된 용기의 내부 온도가 일정하고 입자들의 전체 에너지가 보존된다는 조건하에서 각각의 입자들은 서로 다른 위치와 속도분포를 가지게 되므로 물리적으로 가능한(probable) microstate의 경우의 수가 수없이 많아지게 되는데 이러한 상황을 통계 확률적으로 고려해 보자. 현실적이면서도 물리적인 상황에서 용기 내부에는 입자 1몰만 잡아도 6에 10의 23승 만큼의 입자 수에 해당하므로 엄청나게 많은 수의 입자가 들어 있음을 알 수 있다. 하지만 볼츠만 분포에서 확률분포의 형태를 알아냄에 있어서 단지 몇 개만의 입자를 가지고 얻어낸 결과를 많은 수의 입자 사례에 대해 확장하기로 한다.

아래에 요약 작성된 내용은 아래 사이트의 원문을 참조하도록 하자.
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/disfcn.html

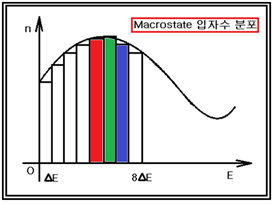
입자가 가질 수 있는 에너지 E를 9 단계로 나누어 단계별로 ⧍E 만큼씩 차이가 있는 것으로 하고 논의의 마지막 단계에서 ⧍E⤍0 으로 극한을 취하여 에너지가 연속적이 되게끔 하자. 고려하는 입자의 수는 단지 N=6개이며 용기 입자들의 에너지의 합은 8⧍E 로 두기로 한다. 물론 6 과 8 이라는 숫자는 임의로 취한 것이며, 대단히 적은 숫자들이긴 하지만 볼츠만 분포의 특성을 알아내는데 충분하다고 보인다.

입자들이 충돌에 의해 에너지를 교환할 수 있기 때문에 microstate 경우 별로 에너지의 합인 8⧍E를 나누어 가지게 된다.

그렇다면 6개의 입자들이 8⧍E 의 에너지를 나누어 가질 수 있는 총 20개의 macrostate를 살펴보자. 실제 체크해 보면 20개가 나오며 어느 macrostate 가 가장 일어날 가능성이 높은지는 차후에 엔트로피와 관련하여 논의 할 것이다.

Macrostate 1 은 6개의 입자 중 5개 에너지가 0 이고 1개가 8⧍E 인 경우이다. 서로 다른 6개의 입자 중에서 5개를 뽑을 수 있는 방법 수는 6!/(5!1!) 즉 microstate 수 6을 가진다. 이 중에서 1개는 8⧍E의 에너지를 가지면 5개는 에너지가 0 이 된다. 볼츠만 분포에서 Macrostate는 MNIST 머신 러닝에서는 특정 class 가 될 것이며 microstate는 특정 class 에 속하는 즉 identical 하면서 distinguishabke 한 수기 문자 샘플들이 될 것이다.

Macrostate 2 는 6개의 입자 중 4개의 에너지가 0 이고 1개가 ⧍E이며 또 1개가 7⧍E인 경우이다. 경우의 수는 6!/(4!1!1!) 즉 microstate 수 30을 가진다.
이러한 방식으로 20개의 macrostate 경우를 다음과 같이 표로 작성해 보자.

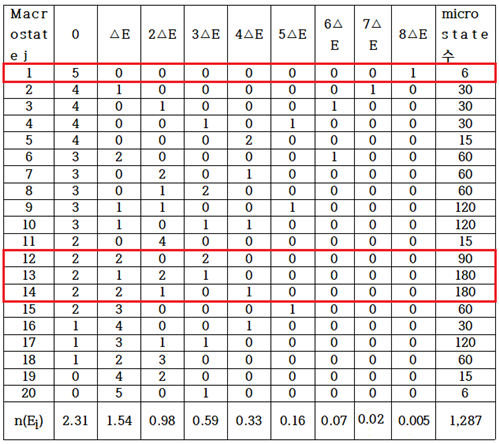
이 중에서 다시 macrostate 6 의 microstate 수를 계산해 내 보자. E=0에 3개 E=⧍E에 2개 E=6⧍E에 1개로 에너지 합계는 8⧍E 이며 일어날 법한(probable) microstate 수는 다음과 같이 계산된다.

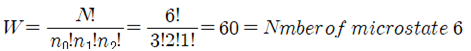
이와 같이 microstate 수를 계산할 수 있으며 아울러 모든 microstate가 일어날 수 있는 확률은 같다고 가정하자. 그렇다면 어느 하나의 Macrostate j가 일어날 확률 Pj는 일어날 수 있는 microstate의 수에 비례하게 된다. 위 표에서 Macrostate는 20개가 있으며 각 Macrostate에 포함된 microstate의 수를 합치면 1287 이 된다.

전체 에너지가 8⧍E 로 일정하다는 조건하에서 얼마나 많은 입자들이 특정 에너지 레벨에 있을지는 Macrostate 별로 각 에너지 레벨마다 계산이 가능하다. 즉 Macrostate 1 에서 E0 = 0 인 레벨에 가장 있을 듯한(probable) 입자의 수는 5X(6/1237)=0.023 개로 계산된다. E0 = 0 레벨에 대해서 20개의 Macrostate 별로 계산하여 합하면 n(E0)=2.31을 얻을 수 있다. 동일한 방법으로 0, ⧍E, 2⧍E, ⦁⦁⦁,8⧍E 에너지 레벨까지 계산이 가능하며 표의 마지막 줄에 결과가 출력되어 있다. 입자들이 가장 있을 법한 에너지 레벨 별 입자 수를 다 더하면 전체 입자 수는 6개가 되어야 한다. 이러한 계산 과정을 다음과 같은 수식으로 표현해 보자.

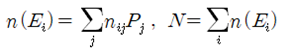
여기서 Pj는 어느 하나의 Macrostate j가 일어날 확률이며, 일어날 수 있는 microstate의 수에 비례한다. nij는 어느 하나의 Macrostate j에서의 에너지 레벨 i에 해당하는 입자 수이다.

이 결과를 다음과 같이 에너지 레벨 Ei를 축으로 하여 점 그래프를 플롯하고 엑스포넨셜 형 곡선으로 curve fitting 한 결과이다.

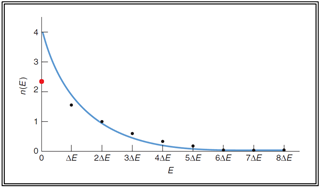
총 입자수가 6개로 적기 때문에 오차가 있을 수 있으나 입자 수를 증가 시키고 에너지 차이 ⧍E를 0으로 보내어 극한을 취하게 되면 굵은 선으로 표시된 엑스포넨 셜 형 곡선 즉

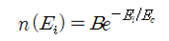
로 어렵지 않개 curve fitting이 가능하다. 이 방정식에서 B 와 Ec는 결정해 주어야 할 상수이며, 에너지 레벨 Ei가 즉 운동에너지로 주어진다면 Ec는 kT 가 된다. k는 볼츠만 상수이며 T는 입자가 포함된 용기의 절대 온도를 나타낸다. 이 함수가 바로 볼츠만 확률분포를 나타낸다. 따라서 각 에너지 레벨에 입자들이 있을 법 한(probale) 볼츠만의 확률은 다음과 같이 normalized 된 형태로 주어진다.

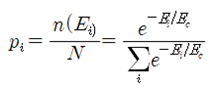
normalization 과정을 통해서 확률분포가 독립변수인 Random 변수인 Ei 의 전체 범위에 걸쳐 확률을 합했을 때 1 이 되도록 한다.

볼츠만 분포에서는 입자의 운동에너지라 볼 수 있는 에너지 레벨 Ei가 항상 양의 값을 가지므로 엑스포넨트의 지수가 항상 음의 값이 되어 에너지 레벨 값이 커질수록 그 확률 값은 감소하게 된다. 반면에 이 볼츠만 분포식을 MNIST 수기문자 인식 이미지 처리 머신 러닝에 적용할 경우에는 그 껍때기에 해당하는 엑스포넨트 형식만 softmax 라는 명령을 통해 취하기로 한다. MNIST 머신 러닝에서 Random 변수인 28X28 = 784 개 픽셀의 값 X는 0∼255 사이의 양의 값을 가지며, 웨이트(W)와 바이아스(b)를 사용하여 볼츠만 분포에서의 에너지 레벨 Ei 에 해당하는 Hypothesis 레벨을 생성할 수 있다. 물리학에서 입자의 운동에너지는 항상 양의 값을 취하나 머신 러닝에서의 아래의 랜덤한 선형적인 Hypothesis 값은 양일수도 있으며 음일 수도 있다.

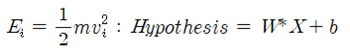
따라서 Softmax 확률분포는 다음과 같이 주어진다.

인덱스 j는 MNIST 데이터 베이스가 포함하고 있는 숫자의 종류 0∼9에 해당하며 i 는 특정한 숫자 class를 의미한다.

물리학과 머신 러닝의 분기점
물리학 적인 관점에서 에너지 레벨 Ei 는 미시적인 양자역학의 세계에서 원자를 들여다 보게 되면 특히 가장 낮은 에너지 레벨의 경우 추가로 파울리의 배타 원리가 적용되어야 하기 때문에 6개 입자의 에너지 레벨 분포 테이블에서 어느 에너지 레벨이라도 2보다 큰 경우는 즉 Macrostate 12, 13, 14를 제외한 모든 경우는 물리법칙을 위반하는 셈이 된다. 따라서 입자수가 2 이상의 probable 한 경우의 수를 제외한 나머지 즉 에너지 레벨 당 입자가 2 또는 그 이하인 입자 분포를 Fermi-Dirac 확률분포라 하며 Sigmoid 함수를 사용하여 표현하며 Logistic Regression에서 중요하게 활용된다. 반면에 모든 입자들이 indistinguishable 하다면 microstate 의 경우의 수가 다 1이 되며 즉 Macrosate 수 자체가 probable한 경우의 수로 남는데 이를 Bose-Eisstein 확률 분포라고 하며 머신 러닝 분야에서는 아직 활용 사례가 없다.

MNIST 문자 인식을 위한 머신 러닝의 과정을 살펴보면 볼츠만 분포와 깊은 관계를 맺고 있음을 알 수 있다. 그 이유는 MNIST 이미지 데이터들의 identical 하면서 distinguishable한 특성 때문일 것이다. 하지만 볼츠만의 확률 분포가 총 입자수가 일정하게 보존 된다 라든가 아울러 에너지 총량이 일정하다는 물리적 개념에 근거를 두고 있지만 반면에 MNIST 문제와 같은 머신 러닝에서는 Hypothesis 설정 과정에 고유의 확률분포를 이끌어 낼 수 있도록 물리학적 조건이 아닌 통계학적인 조건들이 부과되어야 할 것이다.