2-2 Rosenblatt의 퍼셉트론 알고리듬 코딩에 숨겨진 암호를 해독하라?

수년전에 개봉했던 베네딕트 컴보배치 주연의 이미테이션 게임을 관람해 본 적이 있는가? 앨런 튜링의 일대기를 영화화한 이 작품은 사람 나름이겠지만 내게는 뜻 깊은 영화였다. 셜록 홈즈에서 개성이 있으면서 뛰어난 추리 연기를 보여주었던 컴보배치가 천재로도 알려진 알란 튜링 역을 맡아 2차대전 시기에 암호해독을 위해 고심하는 연기는 정말 리얼하게 다가 왔던 것으로 기억된다. 그 이유는 지난해에 구매한 라즈베리 파이에 텐서플로우를 설치하여 머신 러닝에 실질적인 관심을 가져보기도 훨씬 전이었지만 지금의 IT 빅뱅 시대를 열기 위해 오래 전에 뭔가를 파종해야 했던 암호 수학자의 인생에 잠재적인 호기심이 있었던 것 같다.

고되게 일하는 남의 일대기를 영화로 관람하는 것은 그래도 재미가 있다. 하지만 그런 상황을 우리가 직접 맞닥뜨리게 되면 어떤 느낌이 들것인가? 물론 2차 대전 당시의 알란 튜링에게는 독일군의 암호체계 해독작업이 해독이 이루어지기 전까지는 너무나 괴롭고 고생스러운 암담한 나날을 보내는 작업이었을 것이다.

Rosenblatt이 발명한 퍼셉트론 장치에 사용된 알고리듬을 설명하는 오래된 색이 빛바랜 자료를 검색을 통해 찾아내었다. 아래 그림은 Rosenblatt 의 퍼셉트론에 사용된 대표적인 알고리듬인 듯하다. 알고리듬이란 말 어렵게 생각할 필요 없이 우리가 쉽게 이해할 수 있는 코드의 구조 정도로 생각하자.

컴퓨터 언어 방식으로 알고리듬이 간략하게 소개되어 있으나 Rosenblatt 진정한 코딩 의도를 이해하기가 쉽지 않은듯하다.

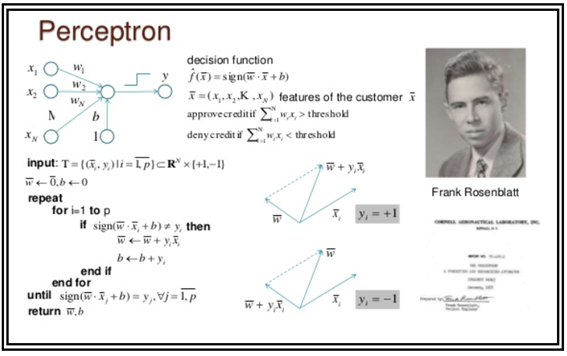
이 자료의 좌측 상단을 보면 Rosenblatt의 이미지 센서 장치로부터 Random한 독립변수로 보이는 xi 가 네트워크에 입력되면 그에 상응하여 역시 Random 해 보이는 웨이트 값들이 곱해져 합산이 이루어지며 아울러 Random한 바이아스 b 값을 더하게 된다.

Decision function으로 정의 되는 아래의 벡터 연산 표현을 살펴보자.

sign() 으로 정의 하는 함수는 웨이트 벡터와 입력 벡터 값을 각각 곱하여 합산하고 바이어스를 더한 값의 부호를 따져보기 위한 함수이다. 수학책에 sign() 이란 함수는 따로 없으며 부호를 판별할 수 있도록 sign() 이란 루틴을 따로 작성해야 한다.

웨이트와 입력을 각각 곱해서 합한 값이 threshold 값보다 크면 신용을 주도록 승인하고 threshold 값 보다 작다면 신용을 거부한다. 즉 threshold 보다 크면 OK 이고 그렇지 않으면 NO 란 뜻이다. 이런 분류를 binary classification 이라고 한다.

이어서 해독이 어려워 보이는 표현이 등장하는데 지금의 MNIST 예제 풀어가는 과정과 너무나 흡사하므로 거꾸로 비교해서 추리해서 풀도록 하자. MNIST를 전혀 모르면 다음에 이어지는 내용이 진짜 풀리지 않는 암호가 될 수도 있음을 사전에 유의하자. 하지만 Rosenblatt 의 코딩 의도를 완전히 이해 못한다고 해서 머신 러닝을 포기할 이유는 전혀 없다. 나 자신도 불과 몇 주 전까지만 해도 결국 오늘날의 MNIST 문제 자체에 대한 제대로된 이해가 없었으며 상당히 교묘하면서도 까다롭고 어려운 문제라는 느낌을 갖고 있었다.

1928년생이면서 1956년에 코넬대에서 박사학위를 받은 다음해인 1957년 Rosenblatt이 발명한 퍼셉트론의 알고리듬을 해독해 보기로 하자.

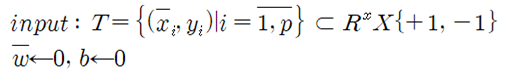
이 문장에서 정수 i 는 1에서 p까지 인덱스 범위를 가지며 좌표의 집합 T는 실수 공간의 원소들이며 아울러 +1과 –1을 원소로 가지는 집합과 관계를 가지게 된다. Rosenblatt 퍼셉트론에 있어서 N 은 400 이며 p 값은 512였다는 점을 기억하자. 즉 p 값은 머신 러닝에서 지정해 주는 학습 횟수에 해당한다. 학습횟수라 함은 MNIST 수기문자 인식 Softmax 문제에서 경사하강법을 적용하기 위한 iteration 횟수에 해당한다.

여기서 xi 와 yi 의 인덱스 i 는 그 범위가 1∼p 인 점으로 보아 입력 백터 데이터와 클라스 벡터 데이터에 대한 iteration 수로 간주한다. 알고리듬 옆의 벡터 연산 그림을 참조해 보면 yi 는 +1 또는 –1 값만을 가짐을 알 수 있다. 따라서 {-1, +1} 표현이 그러한 내용을 가르키는게 아닐까 싶다.

웨이트 벡터와 바이아스 벡터를 각각 0의 값을 주어 초기화 시키자. 이 부분은 MNIST 수기숫자인식 파이선 코드의 헤더 영역에도 zeros 함수를 사용하여 그대로 사용되고 있는 흔적을 찾을 수 있다.

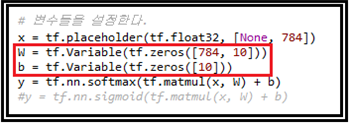
그 다음에 나타나는 repeat은 MNIST 코드의 Session 단계에서의 iteration 에 해당하는 것으로 보인다.

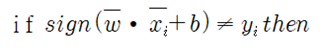
i 번째 학습단계에서 벡터 곱하기 연산 결과가 주어진 threshold 보다 크면 크레딧 +1의 값을 부여하고 yi 와 같은지 비교하자. 이런 비교 작업이 가능하려면 코드 실행 초기 사전에 yi의 값이 즉 다시 말하면 학습 목표 값에 해당하는 달리 말하면 라벨 값이 설정되어 있어야 한다.

yi는 Iris flower 종 분류 문제나 MNIST 수기문자 인식에서 사용했던 클라스 또는 라벨에 가까운 개념을 가진다. 즉 웨이트와 입력을 각각 곱해서 합한 값이 threshold 값보다 크면 클라스 원소중 +1 라벨을 부여하고 그 반대면 –1 라벨을 부여하는 것이다. 많은 수의 입력 데이터에 대해서 이 작업을 하게 되면 자연스럽게 +1 라벨 군과 –1 라벨군으로 분류(classification)가 될 것이다. 아울러 웨이트와 바이아스의 초기값을 0으로 설정한다.

한 페이지 짜리 Rosenblatt 자료에 자세한 설명이 나타나있지 않지만 어떻게 처리하는지 추리해 보도록 한다. Iris 꽃 종 분류 문제 와 MNIST 문제에 대한 이해도가 높을수록 이해가 쉽다는 점을 지적해 둔다.

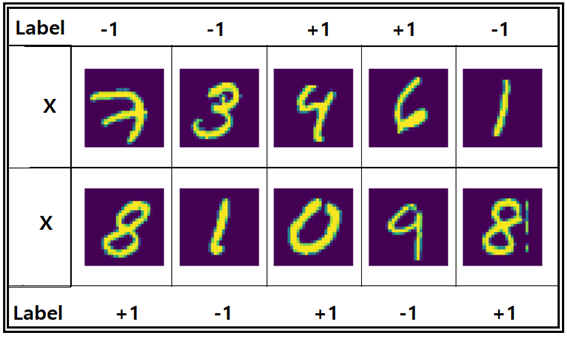
20X20 총 400개의 이미지 센서를 사용한다면 MNIST의 28X28 보다는 해상도가 떨어지겠지만 원리적으로 0, 1, 2,∙∙∙, 9 까지의 숫자 라벨 인식은 충분히 가능할 것이며 Rosenblatt도 이점을 충분히 알고 있었으리라. 아울러 입력 벡터 값 x 도 MNIST에서는 0∼256까지의 숫자로 흑백 명암을 나타내는데 256으로 나눠버리면 즉 normalization 에 의해 0∼1.0 사이의 실수 값으로 표현할 수 있을 것이다.

아울러 일전에 주사위 굴리기 게임에서 짝이 나오는 이벤트에 “1”을 부여하고 그렇지 않으면 “0”을 부여한다는 indicator 변수를 언급했었다. 거의 비슷한 문제로 보면 될 것이다. Rosenblatt이 퍼셉트론 예제의 입력 벡터를 준비함에 있어서 짝이면 “1”을 부여하고 홀이면 “-1”을 부여하는 것으로 정하지 않았나 싶다. 방법은 많으나 가장 간단한 경우를 생각해본 것이다. 라벨데이타를 입력 데이터 종류별로 10가지를 다 택한다면 당시의 컴퓨터 성능으로는 많이 버거웠을 것이다. 그렇게 되면 입력 벡터와 라벨 값이 준비된 셈이므로 머신 러닝 준비가 되었다고 볼 수 있을 것이다.

단 문제는 컴퓨터 성능 한계로 인해 512회 이내에 웨이트 벡터와 바이아스 값을 찾아야 한다는 점이다.

한편 sign함수계산 결과와 라벨 데이터가 일치하지 않을 경우에는 웨이트 벡터를 변경해 가면서 계산해야 하는데 과연 어떻게 웨이트 벡터의 값을 변경할 것인가 하는 문제에 봉착하게 된다. 지금의 MNIST TensorFlow 해법에서는 cost 함수를 구성하여 웨이트에 대한 편미분 계산을 통해 기울기를 알아내고 주어진 learning rate 곱한 양만큼 웨이트 값을 수정하여 안전하게 찾아가는 경사하강법이 있지만 Rosenblatt 시대에 경사하강법이 적용되었던 흔적은 찾아 볼 수가 없다.

다음의 벡터 그림을 사용한 Rosenblatt 의 개념 설명을 해독해 보자. 물론 입력 벡터나 웨이트 벡터가 다차원 변수임에 틀림이 없으나 가시적인 이해를 돕기 위해 3차원으로 생각해서 종이 위에 그림으로 나타내 보자.

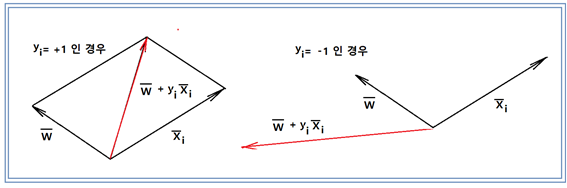
만약 입력벡터가 nomalized 되어 그 벡터의 크기가 1보다 작다면 라벨데이타를 곱해도 역시 크기가 1보다 작기 때문에 512회 연산 후에 웨이트 벡터의 크기가 아무리 커져봐야 ∓512를 넘지는 않을 것이다. 이 그림에서처럼 2차원이나 3차원 벡터를 만들어 실험적으로 작도해 보면 Random한 방향을 가지는 것처럼 보일 것이다.

10개의 이미지 입력 데이타에 대해 512 회 정도의 학습 횟수면 라벨 데이터가 아주 단순하므로 +1 이냐 –1이냐 또는 양이냐 음이냐 정도의 문제이므로 웨이트 벡터와 바이아스 벡터를 충분히 쉽게 찾아낼 수 있을 듯하다. Iris 종 분류 문제를 생각해 보면 된다. 그때는 1936년이므로 주판밖에 없는데도 수 계산으로 종 분류를 다할 수 있었음을 참고하기 바란다.

어랍쇼 해독을 다하고 보니 오늘날 우리가 다루는 MNIST 수기숫자인식 문제의 원조 문제를 그것도 Softmax 확률분포와 경사하강법 없이도 단지 binary classification 이라는 전제하에 그가 다루었던 것이군요. 당연히 성공적인 해답을 내었기에 오늘날의 CNN, RNN 및 언어 번역까지도 가능한 것으로 예상을 하였겠지요!

그렇다면 지난 60년간 인공지능분야에 종사했던 사람들은 암흑기였다고 하니까 몇 명되지도 않았겠지만 아무리 봐도 해놓은 것이 전혀 없다는 판단이 드는군요.

Rosenblatt의 퍼셉트론이 binary classification 문제로 어느정도 이해가 되었으므로 MNIST 수기 숫자인식 문제와 같이 거창한 문제 말고 2개짜리 입력 데이터를 사용하는 퍼셉트론 예제 코딩을 작성해서 다루어 볼 계획이다.