2-13 Logistic regression 에 사용되는 Sigmoid 함수를 사용하게 된 배경을 추적해 보자.

동일(identical)한 하지만 구별(distinguishable) 가능한 입자들의 문제를 다루기 위해 볼츠만으로부터 시작된 통계 물리학은 물리학이라는 경계 내의 볼츠만 분포로 끝나는 것은 아닌 듯하다. 그 이유는 물리학의 범주와 아무런 관계가 없다고 볼 수 있는 머신 러닝 분야가 통계 물리학의 핵심적인 내용을 차용하고 있다는 점일 것이다. 도대체 무슨 소리인가 하는 강한 의문을 제기할 수 있겠지만 이미 볼츠만 분포와 Softmax 기법과의 관계에 대한 논의에서 보았듯이 부인할 수 없는 사실인 듯하다. 다음 사이트 주소에서 기본적인 논의 내용을 참고하기 바란다.

1-22 입자분류를 위한 볼츠만, Bose-Einstein, Fermi-Dirac의 확률분포와 머신러닝 classification 과의 공통점
https://steemit.com/kr/@codingart/bose-einstein-fermi-dirac-classification

이 논의에서 통계 물리학에서 기원한 볼츠만 분포, Bose-Einstein 분포, Fermi-Dirac 분포가 머신 러닝과 뭔가 밀접한 관계를 가지게 된 이유로서 지향 점이 Classification을 대상으로 하고 있다는 점이다. 입자 또는 소립자와 관련된 물리학 연구의 역사를 돌이켜 보면 물질 입자의 근원을 찾아 분류(Classification)해 나가는 과정이란 점에서 머신러닝이 지향하는 Classification과 연관성이 무척 높을 수밖에 없는 것이다.

볼츠만 이후의 통계 물리학의 역사를 체크해 보면 동일한(identical) 입자라고 하는 것들도 구별이 되느냐(distinguishable) 안되느냐의 문제에 부딪히게 된다. 이러한 입자 분류를 위해서는 볼츠만의 방법에서처럼 고전 물리학으로는 접근이 안되며 대안으로서 확률분포함수를 찾아내는 것이 핵심과정으로 자리 잡을 수밖에 없게 된다. 1920년대에 바로 인도의 이론물리학자 Bose가 이런 물리적인 문제를 가장 먼저 연구하기 시작했으며 아인슈타인의 지지를 받게 되어 공동 연구가 이루어졌으며 그 결과로서 Bose-Einstein 의 확률분포가 탄생하게 된다. Bose-Einstein 확률분포의 요점은 2개의 구별이 불가능한 동전 던지기 확률 계산으로 설명이 가능하다. 둘 다 앞면이 나오거나 뒷면이 나올 확률은 각각 (1/4) 이다. 하나는 앞면 다른 하나는 뒷면이 나올 확률은 역시 (1/4)이며 반대의 경우도 확률은 역시 (1/4)이 된다.

이와 같은 확률계산은 2개의 동전이 서로 다른 동전으로서 확실히 구별이 된다는 전제 조건하에서의 확률 계산 결과이다. 그렇다면 2개의 동전이 전혀 구별이 되지 않는다면 확률계산에 어떤 영향을 미칠 것인가?

구별되지 않는 동전을 토스하는 경우 앞면이든 뒷면이든 나올 것이다. 둘다 앞면 또는 뒷면 그리고 하나는 앞면 구별되지 않는 또 하나는 뒷면 이렇게 3가지 경우가 나올 수 있는 것이며 각각의 확률은 황당하게도 (1/3)이 된다는 점이다. Bose 와 Einstein은 구별이 되지 않는 대표적인 사례로 광자를 들었다. 이놈들은 속도도 같고 에너지 레벨도 같고 뭔가 구별할만한 물리적인 요소를 찾을 수 없는 놈들인 것이다. 물론 Bose-Einstein 확률분포와 연관된 구체적인 머신러닝 문제는 아직까지는 없는 듯하다. 이러한 이유로 인해 볼츠만 분포만 해도 그 유도과정이 그리 쉽지 않았기 때문에 지난번 논의에서 그다지 필요성이 제기되지 않은 Bose-Einstein 확률분포와 또 하나 더 Fermi-Dirac 확률분포의 유도 문제를 미루어 두었다.

하지만 머신 러닝에서 가장 많이 사용되고 있는 Logistic regression 확률분포 문제와 관련하여 조사해본 결과 볼츠만 확률분포와 Softmax 확률분포와의 관계에서처럼 확실한 기원을 알 수 없었다. 기이한 일인 듯하다. 모든 학문 분야라는 것이 문헌 서베이를 과정을 거쳐 새로우면서도 창의적인 결과를 얻어내게 되므로 나름의 연속성이나 비연속성이 있기 마련이지만 특히 머신 러닝 분야에서는 모든 것이 아지랑이처럼 흐릿하기만 하다. 그 중에 한가지 볼츠만 분포와 Softmax 와의 관계에 대해선 어느정도 연관성이 충분히 검토되었다고 본다.

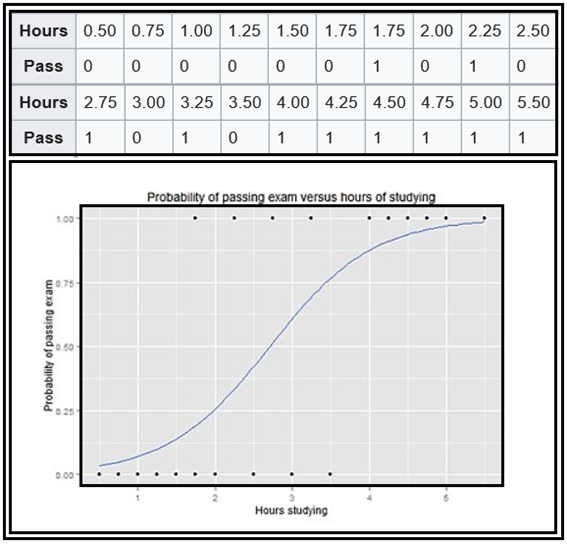
아울러 Bose-Einstein 확률분포와 Fermi-Dirac 확률분포도 머신러닝과 관련이 있지 않을까하는 의구심을 가지고 있었다. 특히 Fermi-Dirac 확률분포는 Logistic regression에서 사용되는 Sigmoid 함수 그 자체이다. 즉 물리학 분야에서 Sigmoid 함수가 도입되어 사용되었다고 봐도 무방한 것 같다. 그럼에도 불구하고 머신 러닝 분야에서 Logistic regression 에 관한 제대로 된 예제를 무슨 이유에선지 찾을 수가 없었다. 기껏 예제라는 것이 학습 시간에 따른 pass/fail 문제 정도이며 머신 러닝 분야에서 세계적인 권위자로 알려진 Andrew NG 교수의 예제는 Tumor 사이즈에 따라 양성인지 또는 악성인지 확률적으로 예측해 보는 문제이다.

특히 pass/fail 예제는 한마디로 넌센스에 해당하는 예제로서 학습시간이 많으면 pass고 시간이 부족하다면 fail 이라는 얘기다. 학습 시간이 애매하면 pass fail 당락이 오락 가락 한다는 스토리며 설사 학습 시간이 과다하게 많다고 해도 fail할 수도 있으며 반면에 학습 시간이 부족하다고 해도 pass 할 수도 있다는 뜻이다. 물론 계산된 확률값을 덤으로 얹어 주니 대단히 멋있는 머신 러닝이라 볼지도 모르겠으나 이런 류의 예제는 있으나 마나한 예제인 듯하다.

강의로 생계를 유지하는 입장이라면 머신 러닝의 Logistic regression 분야를 쉽게 공부해 볼 수 있는 예제로서 적절하다고 평가할지는 모르겠으나 제대로 머신러닝을 배워야 하는 입장에서 보면 최악의 예제인 것이다. 한마디로 머신 러닝을 이해함에 전혀 도움이 되지 않는다는 것이다. 여러 번 거론했던 것처럼 머신 러닝을 제대로 이해하려면 분야별로 제대로 된 똘똘한 예제 하나를 잘 공부하면 그 분야는 이미 끝을 내도 된다는 의견이다.

머신 러닝 분야에서 세계적인 권위자로 알려진 Andrew NG 교수가 드는 예제를 유튜브 동영상 강의 6-1과 6-2를 통해 살펴보자.

그의 Logistic regression 동영상 강의를 다시 리뷰해보는 이유는 강의 내용에 과연 Logistic regression에 어떤 연유로 Sigmoid 함수를 도입하게 된 배경이 무엇인가를 혹 지적하고 있는지 추적해 보기 위함이다.

만약에 영어 듣기가 불편하다면 같은 홍콩과기대 한국계 교수인 Sung Kim 교수의 뛰어난 동영상 강의 5-1과 5-2를 들어도 무방하다. 거의 같은 내용을 비슷한 순서로 해설하고 있다.

Andrew NG의 동영상 강의에 나오는 Logistic regression 예제는 Tumor 사이즈에 관한 예제로서 크기에 따라 악성인지 양성인지를 예측해 보는 문제이다. Tumor 환자로서 병원 치료를 받게되면 기본적으로 MRI 사진 촬영을 하게 되며 이 사진을 바탕으로 종양이 크기를 측정할 수 있다. 최근 작고한 미국의 상원의원 맥케인 상원의원의 사망원인도 악성 튜머로 알려져 있다.

Andrew NG 교수의 이진 분류(binary classification)예제로서 다음 3가지를 들고 있다.
● Email: spam or not spam?
● Online Transactions(정상적인 온라인 거래): Fraudulant(사기성 거래) (Yes or No)?
● Tumor: malignant(악성) or benign(양성)?
이메일에서 스팸처리는 실용성이 답보되는 상당히 중요한 예제가 될 수 있지만 실제 교과서에 예제로 등장하지 않는데 즉 어느 정도 난이도가 있는 응용문제로서 쉽게 설명하기에는 어려움이 있다는 의미이다. 정상적인 온라인 거래인지 또는 사기성 거래인지 판별 문제도 여러 가지 요인이 복합적으로 작용하는 다소 복잡한 문제일 것이다. 세 번째 악성 종양 문제는 우리도 일상 생활에서 부딪힐 수밖에 없는 문제로서 담당 의사와 환자가 함께 고민할 수밖에 없는 문제로서 종양의 크기가 자람에 따라 중요 파라메터로서 임계치가 될 수 있다. 그밖에 많은 유전적인 요인들이나 내분비 문제를 포함하게 되면 너무나 복잡해져 환자가 얼마나 오래 생존할 것인지 예측하기가 오히려 어려워 질 것이다.

y는 머신 러닝에 있어서 클라스 변수에 해당하며 2개이 라벨 값 “1” 과 “0”을 가진다고 보면 된다. 라벨 값 “0”은 benign tumor 즉 양성 종양으로서 환자가 생존 가능한 경우이며 반면에 라벨 값 “1”은 아성 종양으로서 환자의 생명이 위험한 상황을 뜻한다. 라벨 값 “+1” 과 “0”을 가진다는 점은 Rosenblatt 퍼셉트론에서 “+1” 과 “-1”의 라벨 값을 가진다고 하는 것과 별반 차이가 없다. 단지 여기서는 라벨 값을 “+1” 과 “0”으로 설정하지만 실제 확률분포의 범위도 0.0∼1.0이므로 그 양단의 값을 라벨 학습을 위한 값에 직접 대응 시킬 수도 있다.

2개의 원소를 가지는 클라스 집합을 고려한다. 실제로 병원에서는 더 많은 클라스 원소를 생각할 수도 있겠지만 앞서의 종양의 크기와 임계치 논의에 의하면 2개의 클라스 원소면 적절해 보인다.

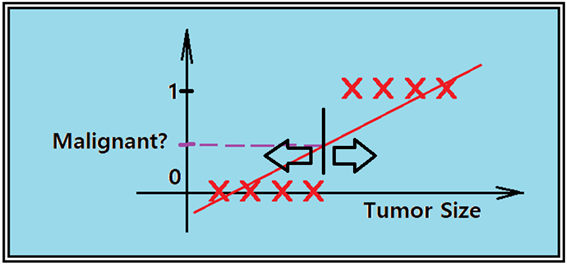
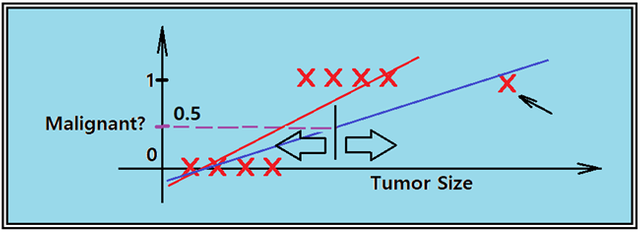
이 문제 분석을 위한 방법으로는 선형회귀 분석을 들 수 있다. x축을 Tumor 사이즈로 두고 적절한 웨이트 값을 도입하여 Hypothesis 직선을 가정하여 최소제곱법을 적용해 풀도록 하자. threshold 가 0.5인 classification 작업을 실시하자. 그림에 표시된 것처럼 선형회귀 직선을 찾을 수 있을 것이다. 필요하다면 바이아스 b를 넣어도 무방하다. 수직선을 중심으로 Tumor 사이즈에 따른 분류가 잘 이루어졌다고 보인다.

반면에 Tumor 사이즈가 대단히 큰 “1” 클라스에 속하는 데이터가 있으면 어떻게 되는지 살펴보자.

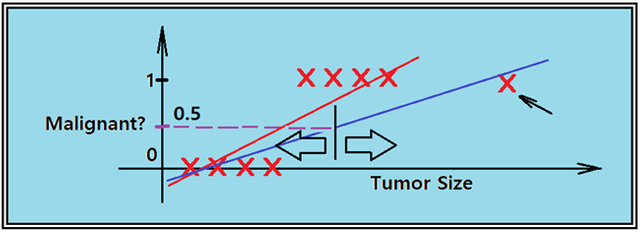
선형회귀 직선의 기울기가 적어지면서 Tumor 사이즈에 따른 악성과 양성 분류가 불투명해지는 듯하다. Binary classification 관점에서 Classifier 직선 윗 부분과 아랫 부분으로 나누어 볼 경우 최대 Tumor 사이즈 데이터가 악성이 아닌 양성으로 분류되는 것은 이 방법에 문제가 많다는 점을 나타내는 듯하다. 아울러 x가 아주 클 때에 Hypothesis 값이 클라스 값인 1.0 을 넘어 버리거나 또는 x가 0에 가까이 가게되면 클라스 값 0.0 보다 작은 음의 값을 가지게 된다. 정리해 보면 선형회귀분석으로는 이 문제를 해결하기 어렵다는 결론이 나온다.

그 대안으로서 0≦Hypothesis≦1.0을 만족하는 Logistic regression을 고려하자. regression 이라고 해서 classification 작업이 잘 안되는 회귀분석법과 혼동될 수도 있으나 Logistic regression은 연속적인 사례 예측이 아닌 아예 그 목적이 분류 즉 classification 에 있다는 점에 유의하도록 하자.

Hypothesis 함수를 hθ(x)=g(θTx)라 두기로 하자. (⋇여기서부터 나오는 그리스 문자 θ는 아래 첨자이며 T는 위첨자인데 마크다운에서 깨져버린듯하니 참고하시기 바람)
여기서 Rosenblatt 의 퍼셉트론에서 W에 해당하는 θ는 웨이트 또는 웨이트 벡터를 뜻하며 x는 입력 벡터를 뜻한다. 위첨자 T는 matrix 의 Transpose를 뜻하며 함수 g의 괄호안의 표현은 퍼셉트론에서 사용하던 벡터 연산 즉 W∙X 에 해당한다고 보면 되므로 계산 결과는 스칼라 값을 가지게 된다..

Logistic regression 에서 사용되는 함수 g는 바로 Sigmoid 함수이며 다음과 같은 그래프 특성을 보여 준다. 즉 z→+∞이면 g(z)→+1.0 이고 z→-∞이면 g(z)→0.0이 된다.
Logistic regression을 위해서는 독립 변수 z를 θTx 로 치환이 가능하다.

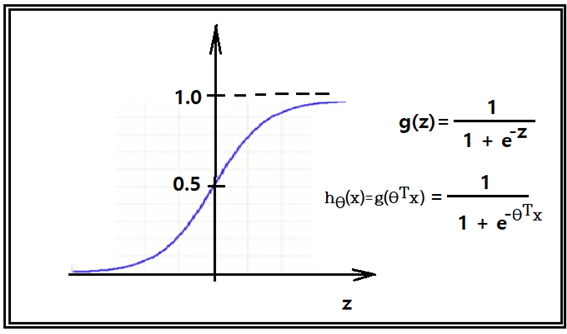
Sigmoid 함수는 모든 실수 z 값의 범위에 대해서 0≦g(z)≦1 이므로 변수 z를 θTx 로 치환 후에는 입력 벡터 x 값의 범위에 대해서 0≦hθ(x)≦1 가 성립한다.

Andrew NG 의 Hypothesis 출력 값을 해석해 보기로 하자. 입력 벡터의 성분은 Tumor 사이즈 즉 크기가 된다. x0 = 1 이란 종양의 크기가 1cm 란 뜻이다. 확률계산 결과 hθ(x)=0.7은 라벨 값 “1”의 상태 즉 악성 종양 상태일 가능성이 70%라는 뜻이다.

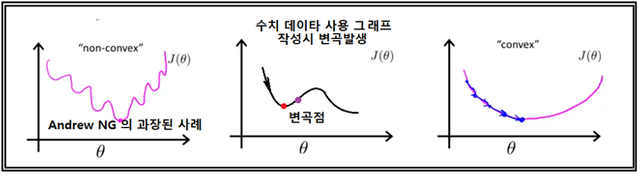
Logistic regression을 위해 cost 함수 구성에서 최소제곱법을 적용하게 되면 cost함수가 독립변수인 웨이트에 대해서 매끄럽게 오목한(convex) 모양을 보여 주지 못하고 주름이 질 정도 내지는 최소한 한번의 변곡이 포함될 경우 참 최소값을 찾아내지 못하고 local minimum을 찾게 될 위험성이 있어 cost 함수를 구성하는 방법을 바꾸어야 한다. Logistic 함수에 여러개의 웨이트와 x 수치 값을 주어 최소제곱하여 그래프를 작도해 보니까 Andrew NG 의 과장된 주름진 모습을 보기는 어렵지만 최소한 변곡을 일으키는 모양을 관찰할 수 있다. 변곡이 있을 경우 경사 하강법 적용에서 learning rate 값이 지나치게 작으면 local minimum을 찾고 끝나버릴 우려가 있다.

log 함수를 사용하여 Logistic regression을 위한 cost 함수를 구성할 수 있다. y=1 즉 라벨 값이 “1”일 때 기준으로 hθ(x) 값이 1.0에 접근함에 따라 cost 함수의 값이 0에 접근하면 바람직하다. 반대로 hθ(x) 값이 0.0에 접근함에 따라 cost 함수의 값이 +∞ 에 접근하면 바람직하다.

반면에 y=0 즉 라벨 값이 “0”일 때 기준으로는 hθ(x) 값이 0.0에 접근함에 따라 cost 함수의 값이 0에 접근하면 바람직하다. 반대로 hθ(x) 값이 1.0에 접근함에 따라 cost 함수의 값이 +∞ 에 접근하면 바람직하다.

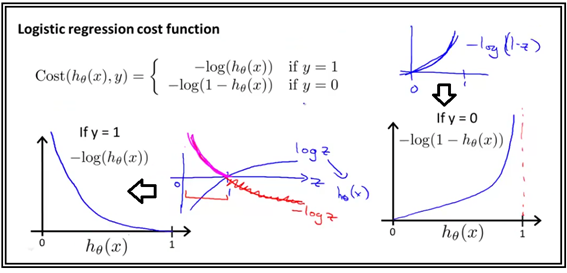
이러한 요구조건들을 만족하는 cost 함수는 if 제어문을 사용하여 처리할 수도 있으나 y에 관한 1차식 형태로 선형 조합하면 1개식으로 표현이 가능하다.

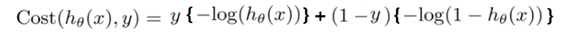
이상의 과정이 Logistic regression 에 관한 Andrew NG 의 강의 내용으로 머신 러닝에 필요한 모든 요건들이 적용되어 TensorFlow 로 코딩하여 문제를 풀 수 있는 준비가 되었다. 코딩 예제는 앞으로 나올 내용 중에 포함시킬 계획이다.

Andrew NG 교수의 동영상을 요약해 보았는데 Logistic regression 작업에 있어서 Sigmoid 함수가 적합한 후보라는 간단한 설명은 있었다. 하지만 Tumor 사이즈를 파라메터로 한 Logistic regression 작업에 있어서 Sigmoid 함수의 도입의 필연적 배경에 대한 의문은 해소되지 않은 듯하다. 이 Tumor 사이즈 문제 해결을 위해서 Sigmoid 함수가 적합할 수도 있겠지만 또 다른 확률분석법인 Softmax 가 더 나을 수도 있는 문제 아닌가?

Tumor 사이즈에 의한 Logistic regression 예측법이 실제로 의학 분야에서 적용되고 있겠지만 Logistic regression의 특성을 알기 쉽게 설명하기에는 미흡해 보인다.
어차피 공식 자체가 Fermi-Dirac이 물리학적 성취로부터 유래되었다면 차라리 물리 문제를 예제로 삼는 것이 나을 듯하다. 고교과정의 물리 화학 교과 과정을 체크해 본 결과 원자 구조의 간단한 양자역학적 확률 특성들이 기술되고 있으므로 물질의 원자 구조 사례 예제를 공부하는 것도 좋은 방법인 듯하다.

짧은 기간이긴 하지만 지금까지의 조사 결과를 보면 머신 러닝의 특히 Classification 은 80년 전부터 통계학과 관계를 맺었으며 볼츠만 통계역학의 확률계산법을 차용한 Softmax 기법은 언제부터 누구에 의하여 시작된지는 명확하지 않다. 아울러 Fermi-Dirac 확률분포를 차용했다고 보이는 Logistic regression 도 그러한 점에서는 동일한 맥락인 듯하다.